2. Random process (Wiener Process) and Model setting
(a) Wiener Process
講Random process點可以唔提Wiener Process
大家可能心諗呢個係乜撚野
但係如果我話比大家聽Wiener process又名Brownian Motion嘅話 大家會唔會即刻覺得好熟口面?
冇錯 如果大家高中有take physics嘅話 其實應該一早就聽過
Particles嘅movement就係Brownian motion嘅一個例子 其實根本就係Wiener Process
(P.S. Particles嘅movement當然係3D Brownian motion, 而我地for simplicity sake只會討論2D嘅Wiener process)
至於佢嘅formal definition就請睇下圖
大家唔好比啲符號嚇親
其實Wiener Process最主要有三個properties
1.) W(0) = 0 (Initial value一定要係0)
2.) Independent increments (e.g. W(4)-W(3) 同 W(2)-W(1) 呢兩舊野係independent)
3.) W(t+h) - W(t) ~ N(0,h) (每一舊increment都係follow normal distribution)
下圖係一個visualization (p.s. 其實呢幅圖嚴格黎講係
唔岩 下面會講點解)
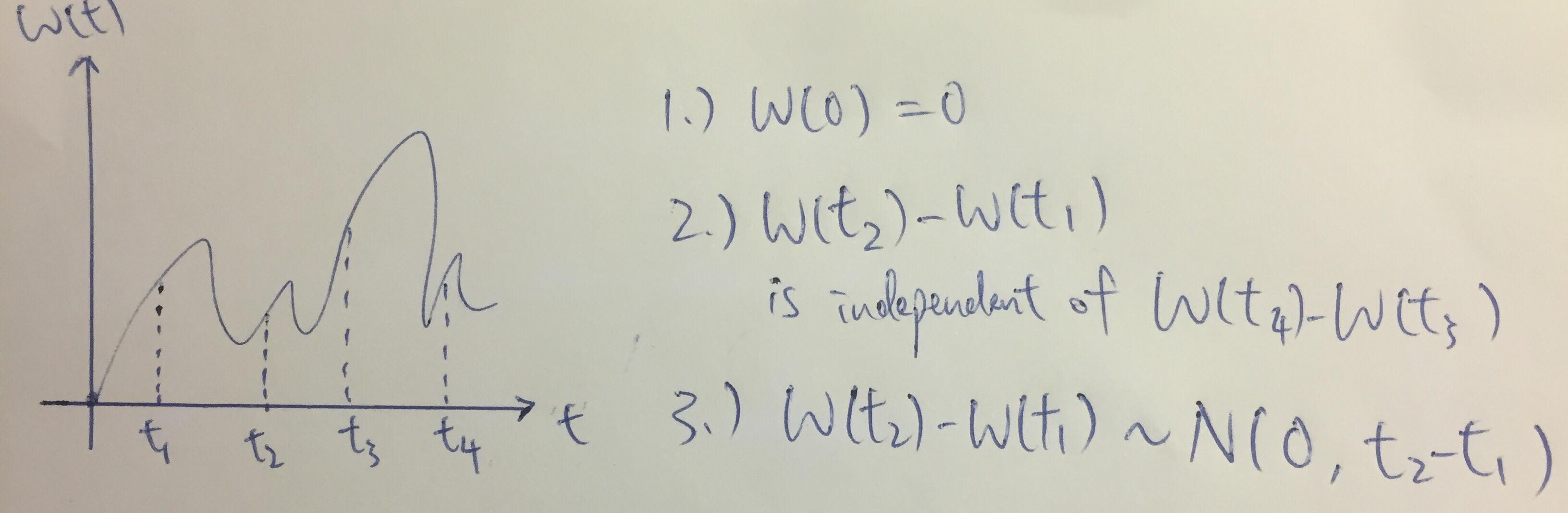
有上面嘅definition之後 我地同時都知道每個increment嘅一啲property
1.) E[W(t+h) - W(t)] = 0
2.) Var[W(t+h) - W(t)] = h
3.) W(t+h) - W(t) ~ N(0,h)
所以我地都可以整到下面呢一句statement出黎
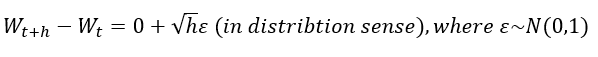
呢一個rephrase嘅concept係後面係
非常重要 希望大家之後會記得
--------------------------
(b) Problem with Wiener Process
到依家為止 世界都仲係非常美好
我地基本上已經有齊曬所有我地應該知嘅野 (distribution, mean, var, independent increment)
如果大家仲記得introduction我講過stochastic calculus其實都係考慮緊類似rate of change嘅問題
咁點解我地唔consider下 dW(t)/dt 呢個物體呢?
但係咁多位 好不幸 最痛苦嘅問題終於出現
如果你wiki過wiener process 都應該會知道佢另外仲有一個好恐怖嘅property
"... However, it can be shown that with probability 1 (almost surely), that a Wiener process is nowhere differentiable, so the term dW(t)/dt cannot be defined..."
大家係咪覺得我已經可以收皮
搞咁撚耐 睇完咁多野原來唔d得? 咁呢舊野可以有乜用?
首先我想大家理解一下乜叫continuous but nowhere differentiable先
一條function點先叫做continuous? 我地可以用一個好naive嘅想法去諗
如果我可以用一支筆 將呢條function f係紙上面畫出黎
而過程中我支筆係冇離開過張紙
咁呢個function f 就係continuous
大家可能已經發覺 continuous but nowhere differentiable其實係好撚痴線
明明你in theory係可以筆不離紙咁畫到條function出離
但係佢又要nowhere differentiable 咁即係全條function都係尖角
但係每個尖角都剩係得最尖個點係not differentiable (諗返|x|係x=0嘅情況)
我要令到全條f都not differentiable就要將每隻尖角嘅兩條邊縮到無限細 得返最尖個點
但係咁樣點有可能畫到出黎????
冇錯 Wiener process就係一樣咁痴線嘅物體
我地就算用電腦sim都只可以approximate佢 更唔好話用手畫出離 (所以我先話上面個幅圖其實係錯)
下面就係一幅用電腦sim出離嘅圖 大家可以見到有幾難畫
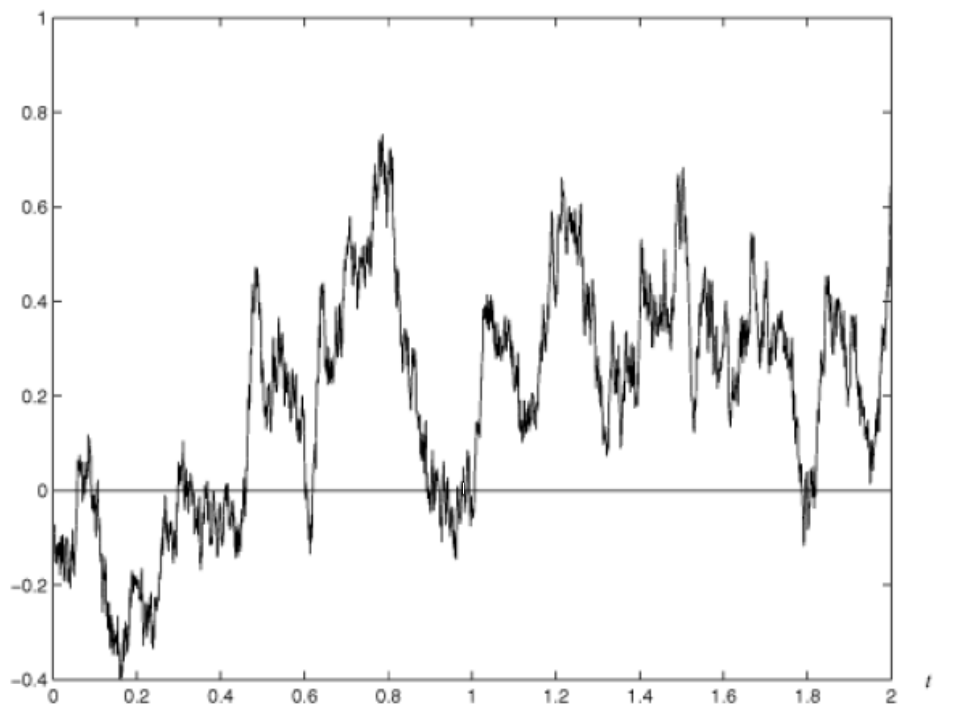
咁最關鍵嘅問題離啦 既然都唔d得 咁呢個process有乜用?
如果你以為唔d就冇用你就太睇少數學家同物理學家
跟住我就會講究竟點樣make use of 呢隻怪物
--------------------------
(c) Basic setting
講咗咁耐wiener process 我地係時候focus返我地究竟想做啲乜
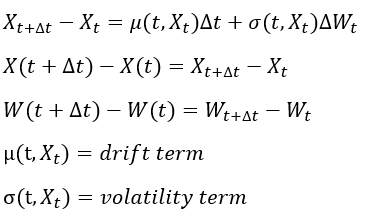
講到尾我地就係想用一d model去model stock price, interest rate呢一類複雜嘅random process (點解複雜? 因為佢地各自都depends on 非常多野)
從而model埋依靠呢堆underlying asset發展出黎嘅derivatives (options, bonds e.t.c.)
而上圖就係我地interested嘅model/setting
大家可以當X係log return of stock price (點解用log return? 大家不如諗下係呢個model底下用% return會有乜問題
)
而X(t+Δt) - X(t) 就係change in log return
大家可以見到change of return 係depends on 兩舊野
第一舊μ我地叫 drift term 大家可以籠統地當係類似change of return嘅mean
(P.S. 值得留意嘅係 呢個drift term係deterministic 而且可能會depends on X 所以係可以整到好複雜
)
而第二舊σ我地叫 volatility term (diffusion term) 大家同樣可以照字面咁解 籠統咁當佢係volatility (standard deviation)
(P.S. 同樣地 呢個term同drift一樣 都係可以depends on X)
而點解X會係一個複雜嘅random process? 就係因為volatility term後面係乘埋一個wiener process嘅increment 另到X有randomness
(Math/Physics友其實可能會知 上圖其實係非常似diffusion)
咁好啦 我地有咗個setting 咁跟住應該點做?
正常如果我地想搵rate of change 我地要做呢兩樣野
1.)將全條equation divided by Δt
2.) Δt -> 0 (Take limit)
但係上面個part先講過 dW(t)/dt係唔exist 咁可以點做?
Simple, we just abuse the notation
我地首先skip咗 step 1, 然後直接入step 2 take limit (Δt -> 0)
咁我地嘅setting就會變咗好似下面幅圖咁
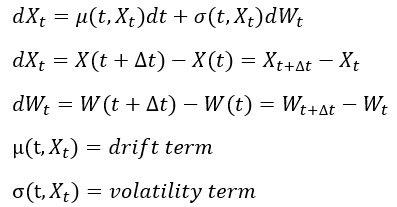
而如果我地比埋一個initial condition比X (e.g. X(0) = a)
咁我地就可以叫全條式做
"Stochastic differential equation"啦
----------------------------
今日應該出住咁多先 跟住就會開始打第一個大佬 --- Ito's lemma
當然係講ito's之前仲有小小野要補充同build up 如果有咩唔太明歡迎留言發問
: "我當 Y~N(0,1), 你點define dY/dx? 你係咪痴撚咗線呀?
"
呢個容後再講 )
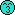
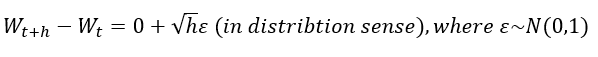
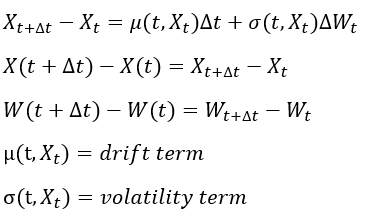
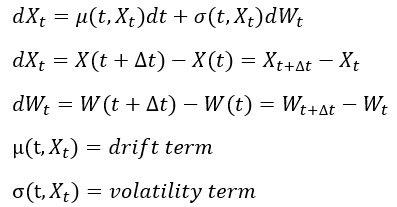
以前做過option pricing