我所知就係決鬥就係當時學術界運作嘅方式
無話點解唔點解
就好似做拳手就要上擂台打過 踢波就落球場比過咁
要贏就要識一啲對手唔識嘅嘢
所以自己有新發現就會收收埋埋唔想俾人知
但咁樣對整個人類無好處
[DSE 2019] 你地溫 數學 又溫成點呢? [7]
dse杏林
1001 回覆
7 Like
9 Dislike
最難既first principle題目係咩
natural log
話說 點解唔會有兩個product乘埋一齊既題目

未有
https://en.wikipedia.org/wiki/Indeterminate_form
無限x零 係所謂嘅 indeterminate form
即係乜都有可能
可能有 limit 又可能無 limit
如果有 limit 嘅話又可以係任何 value
要進一步分析先可以做落去
(L'Hôpital's rule 就係其中一個處理 indeterminate form 嘅工具)
你發現咗其中一個 無限x零 嘅 form 出到 1 其實無咩意義
你可能之後又會發現另一個 無限x零 嘅 form 出到 2
可能之後又會發現另一個 無限x零 嘅 form 其實係 diverge
再者 無限x零 只係一個 form
唔係真係當無限係一個數咁睇 再將佢乘以零等如1
(btw 如何處理無限的確可以係一個有趣嘅議題)
無限x零 係所謂嘅 indeterminate form
即係乜都有可能
可能有 limit 又可能無 limit
如果有 limit 嘅話又可以係任何 value
要進一步分析先可以做落去
(L'Hôpital's rule 就係其中一個處理 indeterminate form 嘅工具)
你發現咗其中一個 無限x零 嘅 form 出到 1 其實無咩意義
你可能之後又會發現另一個 無限x零 嘅 form 出到 2
可能之後又會發現另一個 無限x零 嘅 form 其實係 diverge
再者 無限x零 只係一個 form
唔係真係當無限係一個數咁睇 再將佢乘以零等如1
(btw 如何處理無限的確可以係一個有趣嘅議題)
或者佢應該提醒你
lim (xy) = (lim y)(lim x)
可以咁拆嘅前提係 lim y 和 lim x 兩者均 exist
所以 (lim 1/x)(lim sin x) = lim (1/x sin x) 本身就係唔成立
lim (xy) = (lim y)(lim x)
可以咁拆嘅前提係 lim y 和 lim x 兩者均 exist
所以 (lim 1/x)(lim sin x) = lim (1/x sin x) 本身就係唔成立

原來m1有幾題都會有少少differential equation概念

出親都唔慌難啦
多數送分
多數送分

17年果題原來佢係改到係唔使你solve 個first order 直接俾個答案你去做反落去 唔明係真係會做到但唔會知做緊咩
唔明係真係會做到但唔會知做緊咩
 唔明係真係會做到但唔會知做緊咩
唔明係真係會做到但唔會知做緊咩所謂 0+ 同 0- 相信係指 right hand limit 同 left hand limit
而 limit exist 係需要 right hand limit 同 left hand limit 均 exist 而且相等
但同 lim (xy) = (lim y)(lim x) 嘅前提係 lim y 和 lim x 兩者均 exist 唔同
或者你可以講下點解你覺得兩者有關係
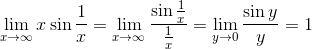
呢個做法無問題
咁做就唔係用 L'Hôpital's rule
比較簡單直接
而 limit exist 係需要 right hand limit 同 left hand limit 均 exist 而且相等
但同 lim (xy) = (lim y)(lim x) 嘅前提係 lim y 和 lim x 兩者均 exist 唔同
或者你可以講下點解你覺得兩者有關係

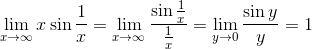
呢個做法無問題
咁做就唔係用 L'Hôpital's rule
比較簡單直接
你係指邊一題

最尾果題
我無聊solve反個first order ode 真係會做反佢俾條式
我無聊solve反個first order ode 真係會做反佢俾條式

做得返佢俾嗰條式唔係好理所當然的嗎
做唔到反而先係出事
btw 其實要「知道做緊咩」
要識嘅唔係 ode
而係 logistic function
https://en.wikipedia.org/wiki/Logistic_function
M1 (加埋以前嘅 math & stat) 已經考咗好多次 logistic model
考生事先見識下可能會比較好

做唔到反而先係出事

btw 其實要「知道做緊咩」
要識嘅唔係 ode
而係 logistic function
https://en.wikipedia.org/wiki/Logistic_function
M1 (加埋以前嘅 math & stat) 已經考咗好多次 logistic model
考生事先見識下可能會比較好

 果題我覺得最難就係學生好少見到左邊有x 右邊有x
果題我覺得最難就係學生好少見到左邊有x 右邊有x M1既applied 其實都幾有用 但好多時都cut 到唔知邊咁多概念
有興趣嘅可以試下做 math & stat 2010 Q9

1/x 擺明係 diverge to infinity
直接話 lim 1/x 唔 exist 就得
唔使再諗 right hand limit 同 left hand limit
就算真係要講 right hand limit 同 left hand limit
都應該話 right hand limit 同 left hand limit 都唔 exist
所以 limit 唔 exist
兩個 limit 首先要 exist 之後先可以講佢地係咪相等
直接話 lim 1/x 唔 exist 就得
唔使再諗 right hand limit 同 left hand limit
就算真係要講 right hand limit 同 left hand limit
都應該話 right hand limit 同 left hand limit 都唔 exist
所以 limit 唔 exist
兩個 limit 首先要 exist 之後先可以講佢地係咪相等

呢題好正 要整成quadratic 呢題其實有咩來頭
要整成quadratic 呢題其實有咩來頭
 要整成quadratic 呢題其實有咩來頭
要整成quadratic 呢題其實有咩來頭咪就係 logistic function 嘅 property 囉
你睇呢段
https://en.wikipedia.org/wiki/Logistic_function#Logistic_differential_equation

你睇呢段
https://en.wikipedia.org/wiki/Logistic_function#Logistic_differential_equation
又好似係 sor. 我只係記得佢係玩quadratic
sor. 我只係記得佢係玩quadratic
 sor. 我只係記得佢係玩quadratic
sor. 我只係記得佢係玩quadratic