我有啲懷疑老師唔識英文

如果你要分
兄弟
兄妹
姊弟
姊妹
係咁全部都係1/4
但係如果你就咁分
兩男
一男一女
兩女
咁就會係1/4, 1/2, 1/4
但係由於呢條題目係冇分長幼
所以我認為兩者係冇分別
你可以用
前者，或者用後者
反正計出黎都一定會係1/3

照你思路已知有一個男 rule out2女
咪得番2種可能性：
2男 and 1男1女囉
1/2

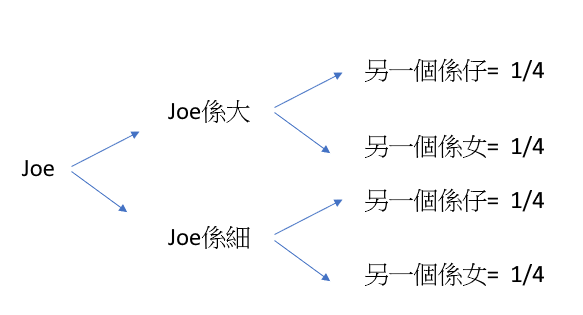
你咁鐘意Tree diagram，我幅Tree diagram對你個弱智嚟講夠唔夠清楚

Fix到AB嘅方法就係根本無AB 其實兩個細佬呢個設定都係廢 就係問你Joe嘅siblings 嘅性別 咁咪就係二分之一

有d 唔同
硬幣既問法係問
下一次佢擲出公/字既機率
咁當然係獨立事件
但係例如我當做人口調查
調查所有兩孩家庭，而且執哂d 已知有一個男既家庭出黎
你會發現，另一個孩子都係男既家庭 佔 執出黎既家庭既1/3

你明唔明你問題係邊 你一邊2男唔分大細 另一邊1男1女你又分大細先變成1/3 你依個叫雙重標準

兩男 1/4 =25%
一男一女 1/2 = 50%
兩女 1/4 =25%

rule out 兩女

兩男/(兩男+一男一女）
25%/(25%+50%)
=1/3

題目set嘅條件全部唔理梗係簡單 但咪會錯
用銀仔就好易明AB嘅重要性
Given一個銀仔係字
同A銀仔係仔
就係1/3同1/2個分別

都話唔係50%，因為其中一半可能性係要排除，因為樓主條題目已經指明邊方係男

又要用大細分？
好， 我就用大細計一次比你睇

B=長男， b=幼男
G=長女， g=幼女
兩孩家庭組合

Bb
Bg
Gb
Gg

夠清楚未？
定你想有同時兩個長男，或者同時兩個長女，定同時兩個幼男，或者兩個幼女？

其實係咪1/2 同1/3都係岩? 睇你點定義"已知"?

下目係google 返黎內容

題目是：一個有兩個孩子的家庭，已知其中一個是女孩，求另一個也是女孩的概率。

這裡其實涉及到語義上的歧義。

答案應該是1/3或1/2，取決於你“已知”的方式。

如果你事先不知道兩個孩子的情況，比如偶然間看到其中一個是女孩，那麼答案是1/2。

如果你是找一個知道情況的人詢問（比如孩子的父母），然後他們告訴你有女孩，那麼答案是1/3。

其實是因為在前一個例子中，你如果看到男孩就直接放棄將其加入樣本空間了，但其實有1/2的概率是“男女”這樣的組合，就會被考慮進第二個例子的樣本空間。

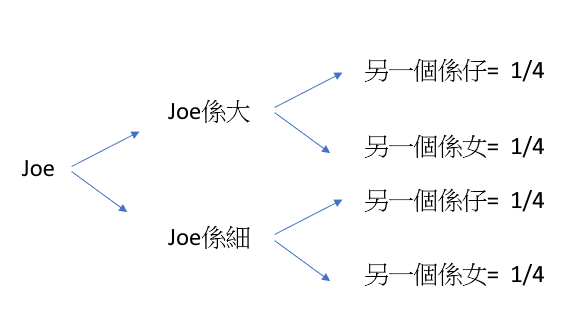
夠唔夠清楚呀

BY CHEATGPT
The probability that Joe's sibling is a brother is 1/2, assuming that the gender of the children is equally likely to be male or female.

To see why this is the case, we can use Bayes' theorem. Let A be the event that Joe has a brother, and B be the event that Joe has a sibling. We want to find P(A|B), the probability that Joe's sibling is a brother given that Joe exists.

We can start by using the fact that there are two possible genders for Joe's sibling: male or female. So we can break down event B into two mutually exclusive events: Joe has a brother (event B1) or Joe has a sister (event B2). Then we can use the law of total probability to express P(B) in terms of these events:

P(B) = P(B1) + P(B2)

Since we know that Joe exists, we can assume that event B has occurred. So we can simplify this equation to:

1 = P(B1) + P(B2)

Now we want to find P(B1|A), the probability that Joe's sibling is a brother given that Joe has a brother. We can use Bayes' theorem to express this in terms of the probabilities we already know:

P(B1|A) = P(A|B1)P(B1)/P(A)

where P(A|B1) is the probability that Joe has a brother given that his sibling is a brother, P(B1) is the probability that Joe has a brother, and P(A) is the probability that Joe has a sibling (which we know is 1).

We know that Joe has a brother (event A), so P(A) = P(B1). And since we assumed that the gender of the children is equally likely to be male or female, we can also assume that P(B1) = 1/2. So we can simplify the equation to:

P(B1|A) = P(A|B1) / 1/2

So now we just need to find P(A|B1), the probability that Joe has a brother given that his sibling is a brother. This is simply 1, since we know that Joe has a brother (event A) and we assumed that there are only two children.

Putting it all together, we have:

P(B1|A) = 1 / 1/2 = 1/2

So the probability that Joe's sibling is a brother is 1/2.

祝你dse好運 無你咁好氣

你係真心覺得你嘅思路係啱？

完全無語義上的歧義，因為唔係是但一個係仔，係已經指明某個係仔

好簡單兄弟就1/4
兄妹 姊弟就弟兩個item
講咗幾多次
如果要分次序 就會有弟兄 兄弟 出現
你唔分次序跟你兄弟1/3 （兄妹/姊弟）1/3 姊妹 1/3
1/3
除
1/3+1/3

好多老師唔只唔識英文 仲唔識思考 同 做人
學以前補習天王Arthur Kho自嘲叻既就唔會教書

所以佢走去炒樓

錄音?

You met Joe. Joe has a sibling. What is the probability that Joe’s sibling is a brother?

你條弱智幾時上水?你唔止弱智，而且好無恥，終於知道自己係弱智唔敢認，第日又繼續老屈人癲而唔記得你自己係點弱智

當一個硬幣係公平情況下
你越擲得多次
個機率會越接近50-50
所以如果你正面個邊機率越趨向1
越唔符合現實
我有理由相信你出千
其實你擲100次 100次都係正面 係極難
正如你係賭場玩21點 拎晒人地4隻A 分4棟
再拎埋4隻king black jack
係
係有可能
但唔符合現實囉

班弱智會話佢可能係大佬有細妹;佢可能係細佬有家姐;可能有兄弟，所以係1/3

Joe想要個 brother都無限接近0%