其實香港好多工overpay
又好多工underpay
好難形容 好多時明明條友做既野唔值咁多但佢又逗咁多
有人做既人值得多d但份糧好似俾人打左7折咁
外國係盡量減到最低掛?
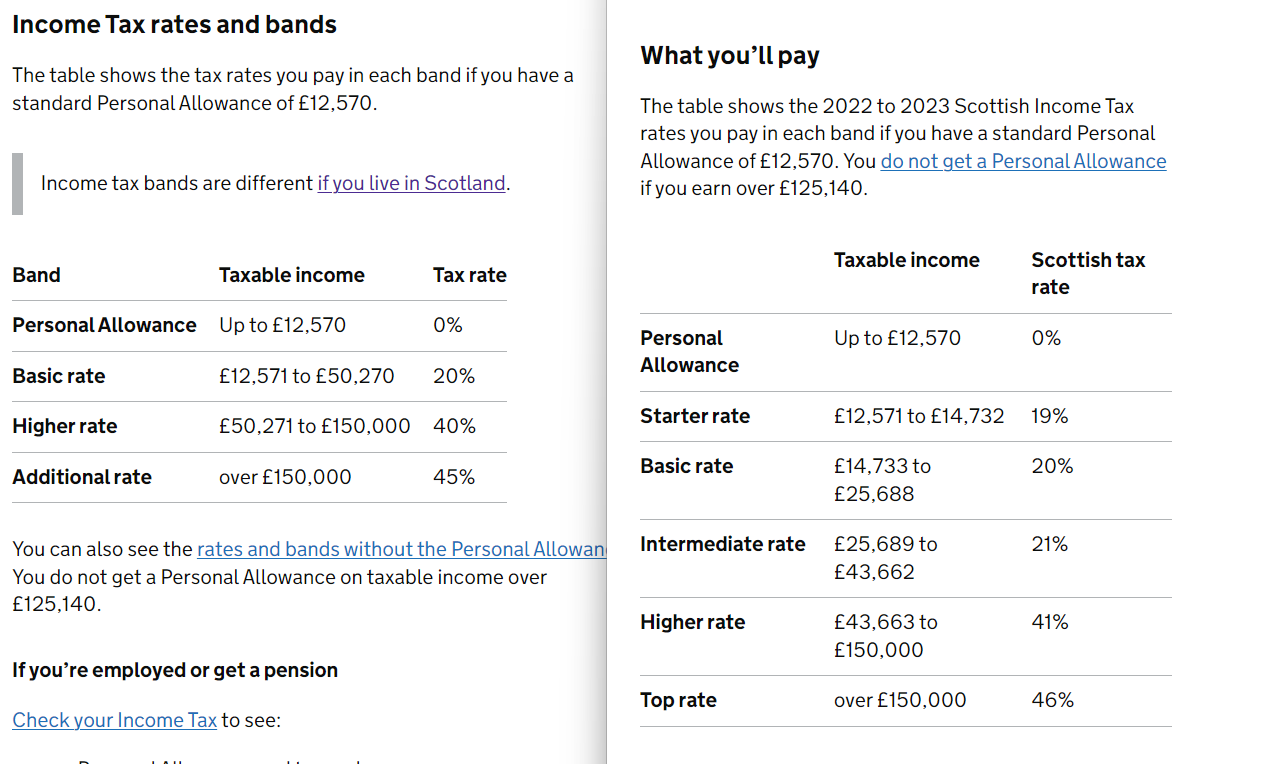
老老實實,英國income tax其實都唔係咁離譜
老鬼屎忽
445 回覆
98 Like
286 Dislike
爬下文啦,我答咗我點計架啦。是旦啦,香港稅係好屈機架啦。我係想講其實英國稅係煩係多,但係未至於好似啲柒頭計都唔計下下40, 45 on99咁計。我就畀緊18.95%, 計埋council計埋NI 大概二十幾,係多過香港架,但其實係咪好恐怖呢,應該唔係。我當年交大灣稅都30幾啦,有幾恐怖呢,政府係咁叫人去就知好嘢啦,下話。三十幾都唔多,二十幾算係乜吖。
衰啲講句係老友你未搵超過£50k先唔覺得英國稅on9
巴打我估我明你講乜,佢年年嗌預繳,嗰陣我喺香港都次次好似要一嘢俾6份1佢咁。無錯係預繳,但你一日唔清稅退休你都要繼續預繳





LM想知佢點有18.95% tax rate

美國都唔撚得
我住LA,
白人區既House 最少1.5m USD
Townhouse 900k
好既Asian 區, House 1.2m
Townhouse 700k-800k
就算你去住Compton槍戰黑人區
最少都要550k
當你俾20%首期,
你月供要3.5k USD


我住LA,
白人區既House 最少1.5m USD
Townhouse 900k
好既Asian 區, House 1.2m
Townhouse 700k-800k
就算你去住Compton槍戰黑人區
最少都要550k
當你俾20%首期,
你月供要3.5k USD



y = 0.4(x - 50270) + 0.2(50270 - 12570)
Substituting y/x = 0.1895, we get:
0.1895 = 0.4(x - 50270) / x + 0.2(50270 - 12570) / x
Simplifying this equation, we get:
0.1895x = 0.4(x - 50270) + 0.2(50270 - 12570)
0.1895x = 0.4x - 20108 + 7540
0.2105x = 12570
x = 59624.4
Therefore, the income is £59,624.40.
To find y, we can substitute this value of x into the third equation:
y = 0.4(x - 50270) + 0.2(50270 - 12570)
y = 0.4(59624.4 - 50270) + 0.2(50270 - 12570)
y = 9420.64
Therefore, the tax paid is £9,420.64.

Substituting y/x = 0.1895, we get:
0.1895 = 0.4(x - 50270) / x + 0.2(50270 - 12570) / x
Simplifying this equation, we get:
0.1895x = 0.4(x - 50270) + 0.2(50270 - 12570)
0.1895x = 0.4x - 20108 + 7540
0.2105x = 12570
x = 59624.4
Therefore, the income is £59,624.40.
To find y, we can substitute this value of x into the third equation:
y = 0.4(x - 50270) + 0.2(50270 - 12570)
y = 0.4(59624.4 - 50270) + 0.2(50270 - 12570)
y = 9420.64
Therefore, the tax paid is £9,420.64.

唉.......終於有人明啦......多謝多謝! 香港稅係低啲架,老老實實,但係認真計個差距未至於好大好離譜,至於vat就更on9,有留意就知唔同貨唔同rate,我都懶得計。睇生活模式啦,本身以前係香港都唔係戈啲係又買唔係又買,空虛到要用購物滿足心靈,生活自在無需要為經濟負擔擔心就最爽架啦,人得一個食得幾多用得幾多?買買買咪又係擺,所以vat影響接近零,貴咗咪當係香港買炒價嘢囉,咪就係買一件半件咁多。
稅真係可以大大聲話外國唔好呀,有數計吖嘛,外國人民水深火熱呀,幾L重稅呀,咁咪有班L屌係度日叫夜叫囉,不過佢地自動屏蔽咗祖國都係重稅咁解。呢邊稅重,啲人都可以屌下政府,或者逼佢再研究下先亂搞。家陣香港一開口就話你立心不良呀抹黑呀危害國家安全呀,呢啲咪就係唔同囉,試下出下聲屌明日大愚吖,睇下點。
稅真係可以大大聲話外國唔好呀,有數計吖嘛,外國人民水深火熱呀,幾L重稅呀,咁咪有班L屌係度日叫夜叫囉,不過佢地自動屏蔽咗祖國都係重稅咁解。呢邊稅重,啲人都可以屌下政府,或者逼佢再研究下先亂搞。家陣香港一開口就話你立心不良呀抹黑呀危害國家安全呀,呢啲咪就係唔同囉,試下出下聲屌明日大愚吖,睇下點。
講起美股mpf,公司係中人壽,當然100% 美股,呢兩年都係跌,但同第二間美股mpf比,佢跌得甘啲,除左有披露嗰十個公司(其實total佔比唔多),都唔知淨低嗰啲係咪去咗買中概股
你自己打份工,儲量用糧單計下啦。又或者咁。當你50000人工,頭12570唔使畀稅。之後戈37430計20%, 即係7486. 咁7486 over 50000 係幾多呀?有冇20%?小學5年級都識計啦,下話。咁其實18.95%點計,你咪代啲數計下囉,好易架咋,小學6年級程度應該識架啦。
咁你LA冇辦法
唔係要住d山卡拉州
非LA、NY既大州都係講緊200幾300萬大屋有游泳池距離市中心半小時內車程
加拿大要咁就真係要去未開發地方先買到
唔係要住d山卡拉州
非LA、NY既大州都係講緊200幾300萬大屋有游泳池距離市中心半小時內車程

加拿大要咁就真係要去未開發地方先買到

*非LA、NY既區
英加嘅銷售稅又唔係買乜都有,食材就無喇,我通常自己煮飯算。
我對你呢段話有啲保留,無錯,喺民主國家可以任屌政府,但唔見得一定研究到解決方案出嚟,有啲支出係歷史留下嘅死症嚟。
下下靠文明選舉可以解決,就唔會有示威啦,反而我覺得西方而家需要一個強硬領袖出嚟,大刀闊斧清下啲瘀血。例如玩TIKTOK班傻鳩,忽略佢哋就啱。
下下靠文明選舉可以解決,就唔會有示威啦,反而我覺得西方而家需要一個強硬領袖出嚟,大刀闊斧清下啲瘀血。例如玩TIKTOK班傻鳩,忽略佢哋就啱。
我對落CHATGPT
佢係咁計錯數
佢係咁計錯數

遲啲應該無喇

私校定state school出首相多?
係,交完呢個“稅”仲比你升值賣樓移英做大爺
真係好委屈
真係好委屈
provisional 都計埋
真係自欺欺人之最
講香港就講mpf
講英國就唔講pension contribution
真係自欺欺人之最

講香港就講mpf
講英國就唔講pension contribution

咁你咁講又唔太公道,唔係個個有錢喺香港買到樓,然後又喺未跌之前賣到樓移民。英國雖然好多問題,但相對於香港樓價低、易買樓對好多人仍然吸引。
人係好現實,如果香港樓價低,生活安穩好多人根本懶得理政治,更加唔會發展到大型示威、國安法、移民潮呢啲事。
同樣班支那人唔畀人封下城、割下韭菜同樣會擁護獨裁共產黨到死。
人係好現實,如果香港樓價低,生活安穩好多人根本懶得理政治,更加唔會發展到大型示威、國安法、移民潮呢啲事。
同樣班支那人唔畀人封下城、割下韭菜同樣會擁護獨裁共產黨到死。
或者啦,當我搵20000,7430要交稅20%,即係畀1486, 得18514落袋,要畀council tax, 要畀NI,計計埋埋其他生活費,20000就真係僅僅夠,冇兩個人一齊分擔下就真係冇乜錢剩。至於係咪得下欄工做,要睇自己啦,其實點都係要想辦法搵份長工做,之後先會有多啲出路。所謂英文好唔好,屌,我返工見到啲印度呀,巴基呀,咪又係尻up然後冇人知佢地講乜,保持開放態度去做啦,首先唔好話自己唔得,同自己講一定要得,冇退路架啦
其實香港人真係唔好用英文唔好做籍口,啲南亞、非洲人口音嚇撚死你,佢哋都做到CS,你無理由唔得

啲示威應該關政治事多過樓價
香港人好忍得

香港人好忍得
