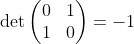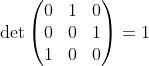[9up數學] 五次方程沒有解?

懷疑入得嚟都係數撚
推廣唔到數學

唔使懷疑， 嚟嚟去去都係嗰啲username

因為對數學會有興趣的得數撚, 唔似phy chem bio

我唔係數撚

fractals抽開左數學除左靚同埋放大果陣會重複出現圖案仲有咩好講?

用Newton formula 屈個答案算唔算

newton's method只可以做到approximation

完左之後會edit好再打出黎

lm

諗起有本故仔書The Equation that Couldn't Be Solved

幫推

一開頭講Field
但連個Field係解咩都睇唔明
係一個可以加減乘除嘅？？？


完全睇唔明


利申：工程撚

你當field係set of rational / real / complex numbers就ok, 我唔會講D騎呢field

set of xxyyzz 即刻明左

4. Permutations

上文講過話呢D洗牌機只係會將d roots調亂
假設 f(x) 係一個 degree n 的polynomial, 而且 f 並沒有重複的roots (係Z, Q, R, C上面, 即係如果f(a) = 0, 則f'(a) =/= 0")
咁 f(x) 會有最多 n 個 roots (每拎走一個root即係拎走一個linear factor, 個degree會減 1)
假如我地將個field加大到包哂 f(x) 所有的roots, 我地就可以label呢d roots做 x_1, x_2, ..., x_n

細心的你就會留意到, 調亂d roots即係調亂 1, 2, 3, ..., n 呢 n個正整數, 所以我地可以將成件事變做:

睇roots點洗牌即係睇點將1, 2, 3, ..., n調亂

記號:

(n_1 n_2 ... n_k)

的意思係
n_1 -> n_2
n_2 -> n_3
...
n_k -> n_1
(如果有更加多數字的話即係其他數字唔郁

例:
(1 4 2) 即係
1 -> 4
4 -> 2
2 -> 1
而3唔郁
如果順次序咁寫即係由 (1, 2, 3, 4) 變做 (4, 1, 3, 2)

如果有兩個呢D痴埋我地會做左最右邊果個先, 然後由右至左咁計, 例如 (1 2)(1 3)(1 4) 即係將 1, 4調左位先
即係由 (1, 2, 3, 4) 變做 (4, 2, 3, 1), 第二個係(1 3), 即係將*更新*左的次序入面的1同3調位, 即係變成 (3, 2, 4, 1), 最後就變成 (2, 3, 4, 1)
有留意的話如果兩個呢種記號的permutations無common的數字的話可以反轉次序, 例如 (1 3)(2 4) = (2 4)(1 3)

用返上面果兩個例子

(a) Q(sqrt{2}) over Q:
如果將
sqrt(2) label做 1
-sqrt(2) label做 2
(i) f(sqrt{2}) = sqrt{2} 即係無洗過
(ii) f(sqrt{2}) = -sqrt{2} 即係 (1 2)

(b) Q(sqrt{2}, sqrt{3}) over Q:
如果將
sqrt(2) label做 1
-sqrt(2) label做 2
sqrt(3) label做 3,
sqrt(3) label做 4
(i) f(sqrt{2}) = sqrt{2}, f(sqrt{3}) = sqrt{3}
即係無洗過
(ii) f(sqrt{2}) = -sqrt{2}, f(sqrt{3}) = sqrt{3}
即係 (1 2)
(iii) f(sqrt{2}) = sqrt{2}, f(sqrt{3}) = -sqrt{3}
即係
1 -> 1
2 -> 2
3 -> 4
4 -> 3
即 (3 4)
(iv) f(sqrt{2}) = -sqrt{2}, f(sqrt{3}) = -sqrt{3}
即係
1 -> 2
2 -> 1
3 -> 4
4 -> 3
即 (1 2)(3 4)

最後要介紹兩個符號: S_n 同 A_n

S_n = all permutations of n numbers.
A_n = all EVEN permutations of n numbers.

咩係even? 最簡單黎講係將n-by-n identity matrix的rows 跟住個permutation黎reorder做一個matrix M, 然後個permutation is even if and only if det(M) = 1. (det(M) = -1的話我地會話個permutation係odd)

例子:
(1 2) 係odd, 因為將identity matrix的 first & second row 倒轉之後,


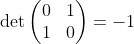
(1 3 2) 係even, 因為



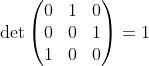
可以證明到
(a) even permutation composed with even permutation = even permutation
(b) inverse of an even permutation = even permutation
(c) identity is even
(實際上只係將佢地所代表的matrices乘埋/take inverse)

(以下可以omit)
(d) odd permutation composed with even permutation = odd permutation
(e) even permutation composed with odd permutation = odd permutation
(f) odd permutation composed with odd permutation = even permutation
(g) inverse of an odd permutation = odd permutation

=====================================

(待續)

Contents:
#1 - Part 1
#9 - Part 2
#115 - Part 3
#221 - Part 3

Errata:
#6: Ignore this

#9: "例如R同Q的algebraic closure係C."
-> "例如R的algebraic closure係C."

#115: "Remark: 如果有學過abstract algebra的話, 如果有個function f: E -> E satisfies (a) & (b), 一係 f 符合 (c1), 一係 f(x) = 0 for all x in E."
-> "Remark: 如果有學過abstract algebra的話, 如果有個function f: E -> E satisfies (b), 一係 f 符合 (c1), 一係 f(x) = 0 for all x in E."

//究竟Gauss同Cauchy呢兩條茂利害左幾多個數學家 lol//

年中幾千幾萬個人寄文比佢，個個都話自己天才，睇漏眼有幾閒
今日既物理系教授都日日收到d天才寄email 黎話自己推翻相對論啦

呢幾日有D野做應該無時間出文住