依家 linear regression 禁個制 / 一句代碼就出結果,而基本教科書都係好直接咁講解 normal equation (正規方程式) 或 maximum likelihood (最大似然) approach,冇詳細咁講點樣 solve normal equation,而教科書又寫住呢條方程式︰
於是就好易產生計算上嘅誤會,即係以為 slope estimator 係透過 inv(Gram(X)) 得出嚟 (注: Gram(X) = t(X)*X)。小妹上次開 post 解釋咗點樣用 SVD 去搵 pseudo-inverse 然後解 normal equation:
[DS141] m2 學生都識嘅 inverse, 實際又有咩用?
- 分享自 LIHKG 討論區
https://lih.kg/3049890
 雖然 pseudo-inverse 比較 stable 同埋通常比直接計 inverse 快,但並冇比 optimized 過嘅 Gaussian elimination 快,因為 pseudo-inverse 係基於 SVD︰
雖然 pseudo-inverse 比較 stable 同埋通常比直接計 inverse 快,但並冇比 optimized 過嘅 Gaussian elimination 快,因為 pseudo-inverse 係基於 SVD︰
 慎防有人問點解唔用 modified Gram-Schmidt 都係因為 accuracy 問題嚟. 當然 Lapack 入面唔止一種方法
慎防有人問點解唔用 modified Gram-Schmidt 都係因為 accuracy 問題嚟. 當然 Lapack 入面唔止一種方法  小妹冇記曬冇睇曬
小妹冇記曬冇睇曬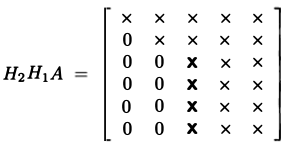


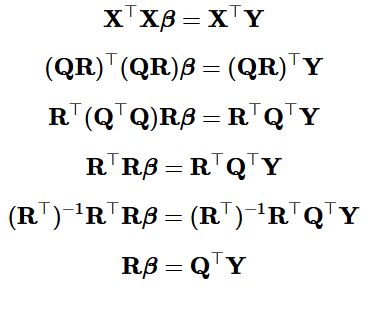
 當 X 係 10^7 by 5 時用 QR 會快 pinv 約 40%, 當 X 係 10^3 by 500 時用 QR 會快 pinv 約 70%, 但 accuracy 差唔多.
當 X 係 10^7 by 5 時用 QR 會快 pinv 約 40%, 當 X 係 10^3 by 500 時用 QR 會快 pinv 約 70%, 但 accuracy 差唔多.
 多謝捧場
多謝捧場


 因為小妹覺得 linear regression 值得深入睇吓點運作,可以睇埋數學上同實際上嘅同異
因為小妹覺得 linear regression 值得深入睇吓點運作,可以睇埋數學上同實際上嘅同異

 米價就靠大家嚟守護
米價就靠大家嚟守護