打錯字都算,張圖都係大陸閪,不過都唔係重點。
重點係份人囂到爆,本身覺得幾好睇又有學術成份,所以果斷正評支持,但批評兩句都唔得。你善意分享唔代表人地唔批評得,個比喻係柒咗仲難明咗,打錯大陸字俾人屌亦正常,樓主個態度真係閪到。
你有料係串得起,但可能只係數學/歷史方面。
著名數學撚系列:地中海沿岸嘅超級英雄
卷殘
118 回覆
525 Like
48 Dislike
公平啲好,你哋可以批評我,我都可以批評你哋唧。
發哥話:我大聲講嘢,唔代表我無禮貌。
咁,我串得起,唔代表我態度閪。
發哥話:我大聲講嘢,唔代表我無禮貌。
咁,我串得起,唔代表我態度閪。
一、絕對可以,但睇你接唔接受訓善意批評,唔知幫唔幫到你進步,但點都有好處。
二、完全唔知講乜鳩。
三、你文字表達、邏輯完全串唔起,再加上態度閪。
數學、歷史我唔知,可能你串得起,但態度一定閪。
二、完全唔知講乜鳩。
三、你文字表達、邏輯完全串唔起,再加上態度閪。
數學、歷史我唔知,可能你串得起,但態度一定閪。
大家忙裡偷閒,交流吓,唔係搵交嗌。
是否善意的批評,值得商榷。不過我唔同意某啲觀點,唔代表我唔接受批評。
例如,你有權表達你睇唔明;我亦可以調低標準迎合你,但係我唔認為咁樣會係進步。
態度閪唔閪係好主觀嘅,如果你覺得唔happy,我真係唔好意思。
我都係嗰句:交流吓唧,唔係搵交嗌。
是否善意的批評,值得商榷。不過我唔同意某啲觀點,唔代表我唔接受批評。
例如,你有權表達你睇唔明;我亦可以調低標準迎合你,但係我唔認為咁樣會係進步。
態度閪唔閪係好主觀嘅,如果你覺得唔happy,我真係唔好意思。
我都係嗰句:交流吓唧,唔係搵交嗌。
講故事幾好
解釋理論就麻麻地
d比喻格硬黎,搞到好難明
解釋理論就麻麻地
d比喻格硬黎,搞到好難明
你用大陸字大陸圖就死返出連登啦,咁撚多廢話,早知唔撚正評你
D性格差撚到

D性格差撚到
我都唔廢話喇.
學術台裡面,大家啲思維可唔可以open啲?
用大陸字大陸圖,同我啲性格有咩嘢關係?
請用文明來說服我。
學術台裡面,大家啲思維可唔可以open啲?
用大陸字大陸圖,同我啲性格有咩嘢關係?
請用文明來說服我。

總之唔理你個態度
問題在於你個比喻真係搞到複雜左
善意提醒 樓主加油

問題在於你個比喻真係搞到複雜左

善意提醒 樓主加油


屌鳩你大陸字咪講句sorry囉
你串乜撚野姐?
宜家大家夾埋黎老屈你咩
個個都屌鳩你就檢討下自己有咩問題啦傻鳩
你串乜撚野姐?
宜家大家夾埋黎老屈你咩
個個都屌鳩你就檢討下自己有咩問題啦傻鳩

你連呢度反簡體字反大陸都未知就學人開post,然後問人地屌你d乜
死返支那啦

死返支那啦
大陸閪





地中海沿岸嘅超級英雄 (3)
嚟到今期最後一篇,要認真啲寫先得。眾所周知,連登仔出咗名難服侍,如果啲數學撚負皮我,呢個系列就好難繼續落去。不過,最驚都係阿基米德條撚樣報夢屌鳩我嘛。
前一篇曲線求證咗圓形面積,今次輪到圓球體體積。論證呢個結果之前,我哋需要3個前設哩。
前設1 - 圓錐體體積 Volume of Cone
史學撚估計年輕的阿基米德曾經到過亞歷山大港留學,而且極有可能响歐幾里得數學院學習。所以肯定條博學撚對歐幾里得嘅《幾何原本》非常熟悉。
《幾何原本》中,第十二章命題7,證明咗:"三角柱的體積等於同底同高的三角錐的三倍。"雖然冇寫到明,但係已經間接求得三角錐的體積喲。
然後,透過「窮舉法」,即係狂咁塞啲三角錐體入個圓錐體裡面,塞到啱啱好就會得出圓錐體體積:
前設2 - 等冪等積原理 Cavalieri's Principle
嗱,親中嘅就叫呢個原理做”祖暅原理”。反共嘅就叫”卡瓦列里原理”囉。(編按:呢度啲人好偏激)
南北朝嘅時候,祖沖之同佢個仔祖暅提出呢個原理,然後求得牟合方蓋的體積,進而算出圓球體體積。
啥,牟合方蓋係咩傢伙?唔睇圖都幾難解釋清楚:
祖氏父子嘅方法比較迂迴,呢度唔詳細講,不過個原理就同700幾年前,古希臘啲數學撚採用嘅概念差不多:「緣冪勢既同,則積不容異。」(編按:摘自《綴術》,已佚失)
睇唔明?試吓英文版-
Cavalieri's principle:The volumes of two objects are equal if the areas of their corresponding cross-sections are in all cases equal.
即係話,如果兩個幾何體嘅所有橫切面嘅面積都相同,咁呢兩個幾何體嘅體積都會係相同。
前設3 - 畢氏定理
呢個唔撚駛我解釋啦啩。
有咗呢3個前設,大家可以數學撚上身,開始推論圓球體體積。
呢項結果最先記載於《球與圓柱論》上卷命題34,當時條撚樣係咁寫:"任一圓球體體積等於圓錐體體積的4倍,該圓錐體以圓球的大圓為底,高為球的半徑。"
轉換成連登仔都睇得明嘅符號,就係:
首先,想象兩個幾何體。第一個,係半徑 = r 嘅圓球體(其實上半球已足夠);第二個,係半徑 = 高 = r 嘅圓柱體,再從中挖空一個圓錐體。
留意幾何體二號嘅體積係:πr^3 - ⅓. πr^3 = ⅔. πr^3
跟住,我哋用等冪等積原理去證明半個幾何體一號,即係上半球嘅體積=幾何體二號嘅體積。
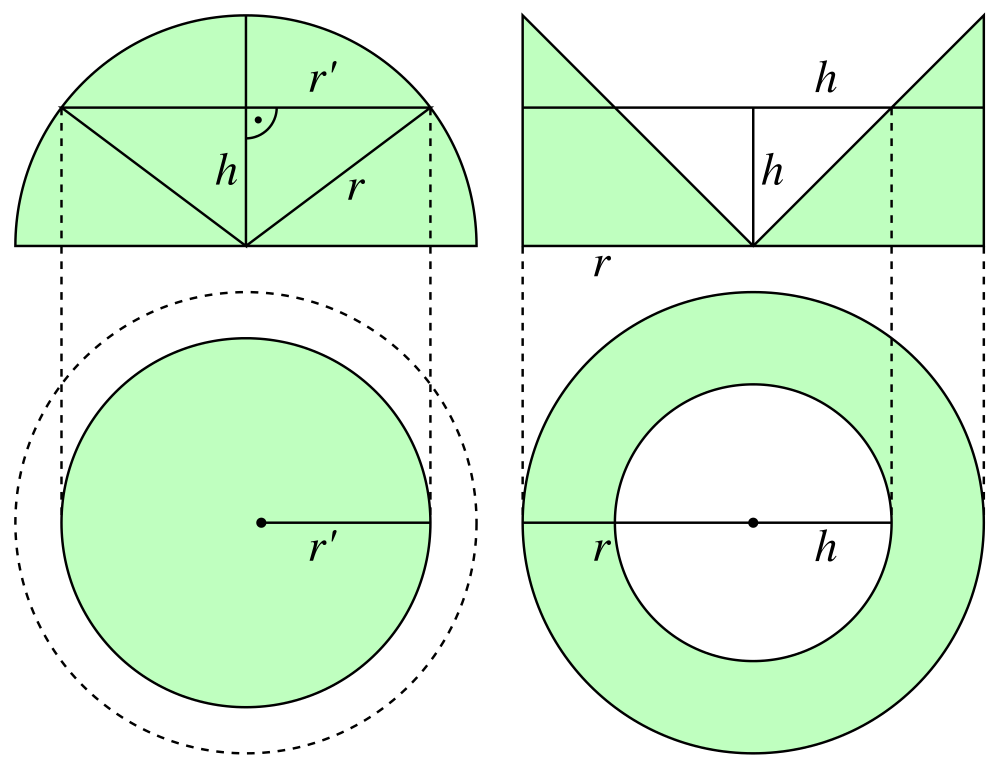
由上半球開始先,搵任何一層離圓心垂直高=h嘅橫切面,咁好明顯係一個比大圓細小小嘅圓形;當佢嘅半徑=r’。
根據畢氏定理,r’ = sqrt (r^2 - h^2),亦即細圓形橫切面面積 = π(r^2 - h^2)。
照辦煮碗,由幾何體二號嘅圓錐中心搵任何一層垂直高=h嘅橫切面,就係一個甜甜圈嘅形狀。因為圓錐體本身係等底等高,所以中空嘅圓形半徑=h。
甜甜圈橫切面面積 = π.r^2 - π.h^2 = π(r^2 - h^2)。
上半球同幾何體二號嘅所有橫切面面積都相同,咁呢兩隻嘢嘅體積就係相同喔。
上半球體積 = 幾何體二號體 = ⅔. πr^3;
登登登櫈,換句話講:圓球體體積 = 4/3. πr^3
多謝大家連日來正皮負皮支持,歡迎數學撚隨時樓下挑機。呢個post呃夠500個like就開新一期,唔夠既話,得閒再開。拜拜。
利申:呢篇啲諧音、懶音、鄉音係我故意加上去嘅,鑑於學術台裡頭「政治正確」同「自我審查」等問題嚴重,而呢啲立場我不能苟同;所以最後—

嚟到今期最後一篇,要認真啲寫先得。眾所周知,連登仔出咗名難服侍,如果啲數學撚負皮我,呢個系列就好難繼續落去。不過,最驚都係阿基米德條撚樣報夢屌鳩我嘛。
前一篇曲線求證咗圓形面積,今次輪到圓球體體積。論證呢個結果之前,我哋需要3個前設哩。
前設1 - 圓錐體體積 Volume of Cone
史學撚估計年輕的阿基米德曾經到過亞歷山大港留學,而且極有可能响歐幾里得數學院學習。所以肯定條博學撚對歐幾里得嘅《幾何原本》非常熟悉。
《幾何原本》中,第十二章命題7,證明咗:"三角柱的體積等於同底同高的三角錐的三倍。"雖然冇寫到明,但係已經間接求得三角錐的體積喲。

然後,透過「窮舉法」,即係狂咁塞啲三角錐體入個圓錐體裡面,塞到啱啱好就會得出圓錐體體積:

前設2 - 等冪等積原理 Cavalieri's Principle
嗱,親中嘅就叫呢個原理做”祖暅原理”。反共嘅就叫”卡瓦列里原理”囉。(編按:呢度啲人好偏激)
南北朝嘅時候,祖沖之同佢個仔祖暅提出呢個原理,然後求得牟合方蓋的體積,進而算出圓球體體積。
啥,牟合方蓋係咩傢伙?唔睇圖都幾難解釋清楚:

祖氏父子嘅方法比較迂迴,呢度唔詳細講,不過個原理就同700幾年前,古希臘啲數學撚採用嘅概念差不多:「緣冪勢既同,則積不容異。」(編按:摘自《綴術》,已佚失)
睇唔明?試吓英文版-
Cavalieri's principle:The volumes of two objects are equal if the areas of their corresponding cross-sections are in all cases equal.
即係話,如果兩個幾何體嘅所有橫切面嘅面積都相同,咁呢兩個幾何體嘅體積都會係相同。
前設3 - 畢氏定理
呢個唔撚駛我解釋啦啩。
有咗呢3個前設,大家可以數學撚上身,開始推論圓球體體積。
呢項結果最先記載於《球與圓柱論》上卷命題34,當時條撚樣係咁寫:"任一圓球體體積等於圓錐體體積的4倍,該圓錐體以圓球的大圓為底,高為球的半徑。"
轉換成連登仔都睇得明嘅符號,就係:

首先,想象兩個幾何體。第一個,係半徑 = r 嘅圓球體(其實上半球已足夠);第二個,係半徑 = 高 = r 嘅圓柱體,再從中挖空一個圓錐體。

留意幾何體二號嘅體積係:πr^3 - ⅓. πr^3 = ⅔. πr^3
跟住,我哋用等冪等積原理去證明半個幾何體一號,即係上半球嘅體積=幾何體二號嘅體積。
由上半球開始先,搵任何一層離圓心垂直高=h嘅橫切面,咁好明顯係一個比大圓細小小嘅圓形;當佢嘅半徑=r’。
根據畢氏定理,r’ = sqrt (r^2 - h^2),亦即細圓形橫切面面積 = π(r^2 - h^2)。
照辦煮碗,由幾何體二號嘅圓錐中心搵任何一層垂直高=h嘅橫切面,就係一個甜甜圈嘅形狀。因為圓錐體本身係等底等高,所以中空嘅圓形半徑=h。
甜甜圈橫切面面積 = π.r^2 - π.h^2 = π(r^2 - h^2)。
上半球同幾何體二號嘅所有橫切面面積都相同,咁呢兩隻嘢嘅體積就係相同喔。
上半球體積 = 幾何體二號體 = ⅔. πr^3;
登登登櫈,換句話講:圓球體體積 = 4/3. πr^3
多謝大家連日來正皮負皮支持,歡迎數學撚隨時樓下挑機。呢個post呃夠500個like就開新一期,唔夠既話,得閒再開。拜拜。
利申:呢篇啲諧音、懶音、鄉音係我故意加上去嘅,鑑於學術台裡頭「政治正確」同「自我審查」等問題嚴重,而呢啲立場我不能苟同;所以最後—

好彩冇㩒定正評
唔係實後悔

唔係實後悔

屌你老尾啲人鑽牛角尖程度同啲小學雞一撚樣
一開始第一篇好地地 雖然1999但睇得出有心思
第二篇事實係複雜左個理論咁 唔明緊係問多兩句同善意批評啦
你就偏要漠視人地批評 你用素質 用殘體字/圖 得! 單機啦

一開始第一篇好地地 雖然1999但睇得出有心思
第二篇事實係複雜左個理論咁 唔明緊係問多兩句同善意批評啦
你就偏要漠視人地批評 你用素質 用殘體字/圖 得! 單機啦

到底直角三角形嗰度係做緊乜鳩
講得仲1999過我 


留名待睇

自己就要懶貼地懶風趣,
點知眼高手低寫到個比喻九唔搭八,
自己又唔受屌嬲嬲豬,
就老屈話呢度自我審查政治正確,
得啖笑,躝返上知乎啦
點知眼高手低寫到個比喻九唔搭八,
自己又唔受屌嬲嬲豬,
就老屈話呢度自我審查政治正確,
得啖笑,躝返上知乎啦
最尾果篇寫得咁晦氣
不如唔好寫啦
辛苦自己又辛苦呢度負皮你既人
Btw 連登一班數學高手見佢咁串
真係笑而不語
不如唔好寫啦
辛苦自己又辛苦呢度負皮你既人
Btw 連登一班數學高手見佢咁串
真係笑而不語

留名
什你老母
睇撚完啦
睇到頭一半都未介紹主角數學野有咩咁勁
超過一半都講歷史
好啦 睇到主角出現啦,又冇講主角d威水野,就咁用乜乜拋物面反射器,你講2個名就知佢數學 物理 工程好勁?
成篇講主角數學物理勁既範圍都唔有冇一成
睇到頭一半都未介紹主角數學野有咩咁勁
超過一半都講歷史
好啦 睇到主角出現啦,又冇講主角d威水野,就咁用乜乜拋物面反射器,你講2個名就知佢數學 物理 工程好勁?
成篇講主角數學物理勁既範圍都唔有冇一成
你知唔知咩叫正治政壓同自我審查












不如叫佢望下負累果篇點寫先
果篇貼地好多
果篇貼地好多
