
[數撚圍爐區] 祝手巴日日無工開, 想出紙永遠失敗 (54)
kai龍(苗撚)
1001 回覆
1 Like
3 Dislike
第 1 頁第 2 頁第 3 頁第 4 頁第 5 頁第 6 頁第 7 頁第 8 頁第 9 頁第 10 頁第 11 頁第 12 頁第 13 頁第 14 頁第 15 頁第 16 頁第 17 頁第 18 頁第 19 頁第 20 頁第 21 頁第 22 頁第 23 頁第 24 頁第 25 頁第 26 頁第 27 頁第 28 頁第 29 頁第 30 頁第 31 頁第 32 頁第 33 頁第 34 頁第 35 頁第 36 頁第 37 頁第 38 頁第 39 頁第 40 頁第 41 頁








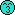

做到咁跟住就唔識了



method of characteristics喎
你目標係solve左條integral curve先
你目標係solve左條integral curve先
條 integral curve (x(t), y(t)) 會satisfy
x'(t) = x(t) - y(t)
y'(t) = 0
而且 u(x(t), y(t)) 會satisfies
(d/dt) u(x(t), y(t)) = 3u(x(t), y(t)) + 2[x(t)]^2
解哂三條ODE就ok
x'(t) = x(t) - y(t)
y'(t) = 0
而且 u(x(t), y(t)) 會satisfies
(d/dt) u(x(t), y(t)) = 3u(x(t), y(t)) + 2[x(t)]^2
解哂三條ODE就ok
唔太關事既野:
1. 用鉛筆
2. 你點由y’=-y/x落下一步的
1. 用鉛筆
2. 你點由y’=-y/x落下一步的
btw in case你唔知堆野點黎...
Given
(x - y)u_x - 3u - 2x^2 = 0
我地可以變做
∇u.(x - y, 0) - 3u - 2x^2 = 0
假設有條curve a(t) = (x(t), y(t))
咁 (d/dt) (u(a(t)) = ∇u.a'(t)
係咪好似第一個term?
所以我地可以set
a'(t) = (x - y, 0)
於是就有我上講果堆野
Given
(x - y)u_x - 3u - 2x^2 = 0
我地可以變做
∇u.(x - y, 0) - 3u - 2x^2 = 0
假設有條curve a(t) = (x(t), y(t))
咁 (d/dt) (u(a(t)) = ∇u.a'(t)
係咪好似第一個term?
所以我地可以set
a'(t) = (x - y, 0)
於是就有我上講果堆野