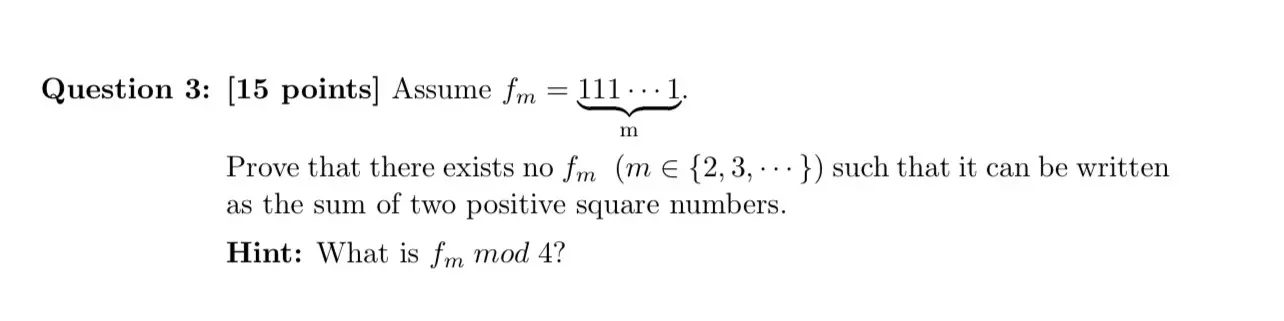
兄弟 check 埋呢題先好訓



To solve this problem, we need to determine the remainder of f_m when divided by 4 and use that to show it cannot be expressed as the sum of two positive square numbers.
### Step 1: Determine f_m modulo 4
The number f_m consists of m ones. For example, if m = 2, f_m is 11; if m = 3, f_m is 111, and so on. This number can be written as:
f_m = (10^m - 1) / 9
To find the remainder of f_m when divided by 4, we first need to calculate 10^m modulo 4. We know that:
- 10 is congruent to 2 modulo 4
- For any positive integer m, 10^m is congruent to 2^m, and since 2^m (for m ≥ 2) is divisible by 4, we get 10^m congruent to 0 modulo 4.
Therefore, 10^m - 1 is congruent to 3 modulo 4.
Next, we calculate f_m as:
f_m = (10^m - 1) / 9
Since 10^m - 1 is congruent to 3 modulo 4, we divide this by 9. Since 9 is congruent to 1 modulo 4, dividing by 9 does not change the remainder, and we still get 3.
So, f_m is congruent to 3 modulo 4.
### Step 2: Sum of Two Squares
To determine whether a number can be written as the sum of two squares, we use the following rule:
- The sum of two squares modulo 4 can only result in 0, 1, or 2. Specifically:
- The square of 0 is 0 modulo 4.
- The square of 1 is 1 modulo 4.
- The square of 2 is 0 modulo 4.
- The square of 3 is 1 modulo 4.
Thus, if a number can be written as the sum of two squares, its remainder when divided by 4 must be 0, 1, or 2, but **never 3**.
Since f_m is congruent to 3 modulo 4, it cannot be written as the sum of two squares. No combination of squares will give a result of 3 modulo 4.
### Conclusion
We have shown that f_m, the number formed by m consecutive 1's, is congruent to 3 modulo 4. Since numbers congruent to 3 modulo 4 cannot be written as the sum of two squares, it follows that f_m cannot be written as the sum of two positive square numbers.
















 好似正路
好似正路 




 3q
3q 
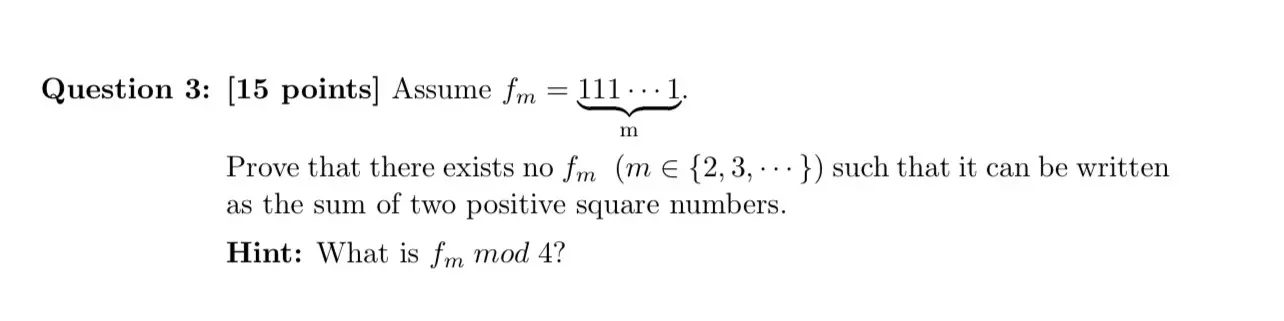 兄弟 check 埋呢題先好訓
兄弟 check 埋呢題先好訓

