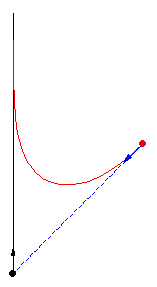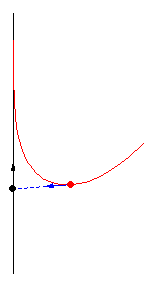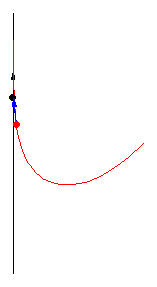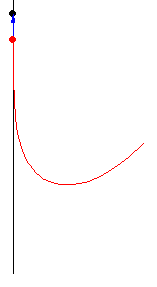
可唔可以唔用微積分解呢條行程問題

algebraic curve嘅path length都唔一定有closed form
所以對於呢個問題，佢係唔係algebraic curve係irrelevant

個答案係咪又係2/3

樓主應該中4左右

可能parametrrize 完用limit去計有某d特別解

中四就學pursuit curve
邊間中學咁勁

文科撚：

https://en.m.wikipedia.org/wiki/Radiodrome

都要用微積分解，最後答案係equation 18

自己真人行一次

係咁樣, 你幻想下D狗點追住你

https://mathworld.wolfram.com/PursuitCurve.html
BTW行乙行過既path係咪L型咁行

係呀! 當甲既速度係乙既整數倍，甲既路線係一條algebraic curve，答案先係咁靚既數字。

甲嗰條path既arclength 咁啱就有closed form, 仲要係polynomial。條path係algebraic curve，同點解個答案咁靚絕對有關係。

係呀

我之前有一兩個post應該暴露左年齡，你一定無睇喇

你都識講咁啱啦
algebraic curve嘅arc length未必有closed form (e.g. ellipse)
而non-algebraic curve嘅arc length都可以有closed form
即係佢有closed form唔係因為佢係條algebraic curve, 而係因為佢satisfy某條differential equation

或者我講清楚少少啦。我指出條curve係algebraic, 係因為之前呢度有人問條curve係咪elliptic curve，同埋似乎現今literature無point out呢個fact

甲既速度係乙既整數倍 iff 甲條path係algebraic iff 甲既arclength係可以用polynomial表示

呢個我覺得係有趣既observation

有興趣黎睇下
https://www.youtube.com/watch?v=d33PwgynXg4&ab_channel=%E9%A4%93%E8%9F%B2