講下 Fourier transform
practical來說用 DFT 多
講 DFT好過
講下 Fourier transform
讀完可做咩
可揸兜
好彩咪餓唔死唔
唔好彩就應該就去做it 好過做細電
利申:做緊 semiconductor
讀完可做咩
可揸兜
好彩咪餓唔死唔
唔好彩就應該就去做it 好過做細電
利申:做緊 semiconductor
贏到四大同學仔入到臺積電就唔同曬



講下 Fourier transform
http://blog.xuite.net/lapuda.chen/PaulBlog/221866406

歡迎黎到數碼世界!
企開D啦屌你老母fuck
正如前面講過, AM FM係將一D連續信號(類比信號)調變再送出, 但係傳送過程中好易受到唔同既Noise影響. 正因為咁, 有人就諗出digital signal 既概念
咁究竟點將一個連續既數號變成digital signal呢? 其實有兩個步驟:
1. 取樣(sampling)
2. 量化(quantization)
首先定義一個period, 隔幾多秒去攞一個sample, 根據sample 既電壓去將佢量化, 定為某一個預先設定好既等級. 將所有既sample 連埋就會得到一個數碼信號. 但上面張圖睇落係咪唔似原始信號? 無錯, 因為數碼信號既還原度取決於你有幾多個量化等級. 假如你用2個bit去量化你D 樣本, 你每個樣本就只有4個等級(00, 01, 10, 11) 可以歸類你既原始信號; 如果係3bit, 就會有8個, 如此類推
而係量化過程中出現既誤差, 我地叫佢做quantization error
當然, 取樣既時間間隔同樣重要. 一般黎講, 如果原始信號既頻率係5Hz (係原始信號 唔係載波), 我地會用原始信號既雙倍頻率(10Hz)去取樣, 咁樣攞出黎既數碼信號就會靚d. 而呢個雙倍頻率我地一般叫佢做Nyquist Rate.
你漏左 clock cycle synchronize
而Nyquist Rate係唔會出distortion (mirror 形成overlap)既最低sampling rate 而唔係下下攞兩倍
Band pass signal低過兩倍都仲得
過兩倍做oversampling 又可以減低SNR


睇開蝗書?
蝗佬唔識字先將訊號訊息通訊叫信號信息通信

有無咩書推介下
你想學邊part讀緊咩科
純粹自學為興趣可以揀臺灣書[black][/black]
有無啲academic 啲,non EE仔想學下嘢
有無咩書推介下
你想學邊part讀緊咩科
純粹自學為興趣可以揀臺灣書[black][/black]
有無啲academic 啲,non EE仔想學下嘢
有無啲introduction 既?你地用開邊本


今次真係很有用
利申:讀緊留名學野

 題外話: 你地覺得50Gb/s 多定少? 如果少, 幾多先夠?
題外話: 你地覺得50Gb/s 多定少? 如果少, 幾多先夠?

Modulation format
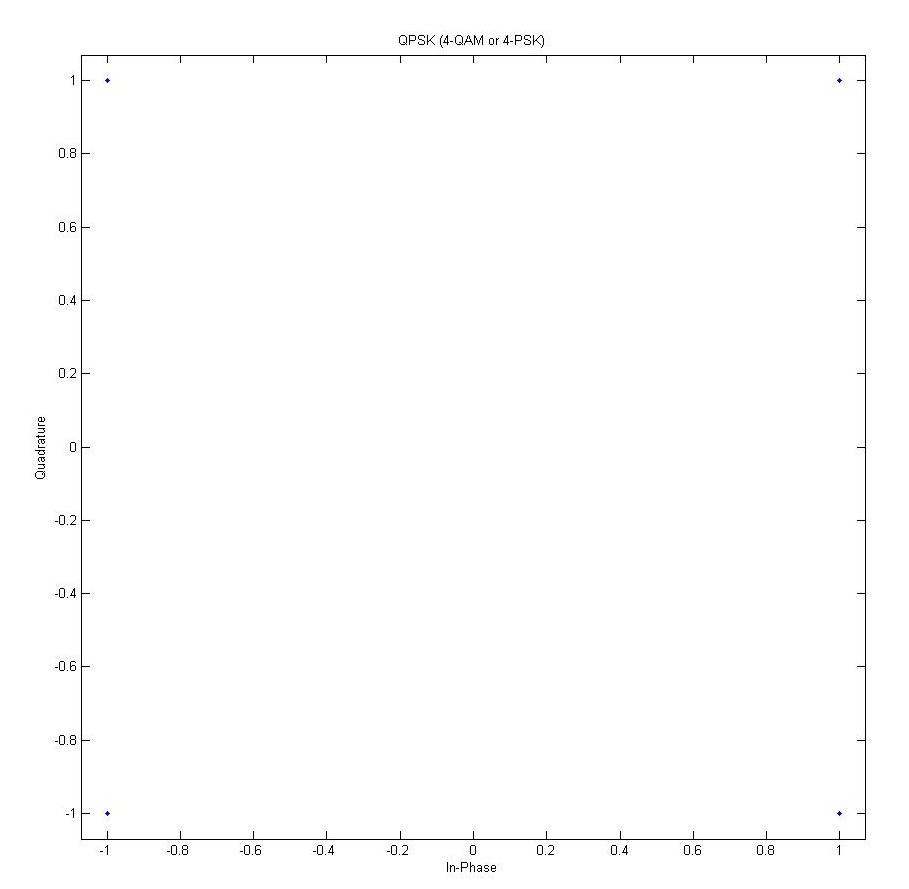
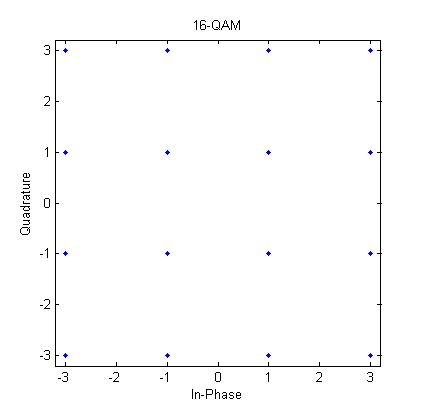
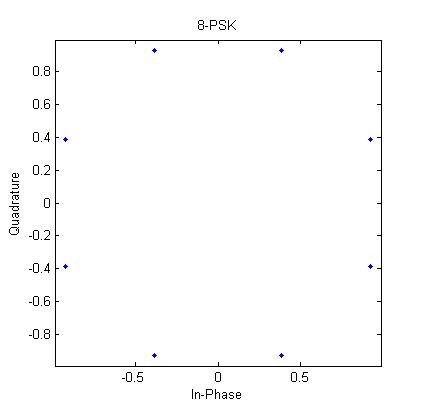
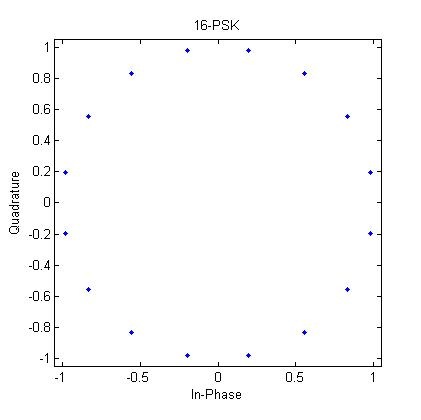
上回講左少少modulation format. 而家主流又經典既modulation format 有兩種, 一隻係QAM, 另一隻係PSK. QAM 大部分就好似上一個post d圖咁四四方方咁, 可以歸類為Square QAM (仲有長方形, 好似8QAM有8粒點)

上面一張係4 QAM, 另一張係16-QAM. 前面既數字代表呢個格式有幾多位置可以放D 點點(symbol). 但好似上一個post咁, 4 QAM係俾人叫慣QPSK, 點解呢? 因為QPSK個4點既magnitude係一樣, 而所有symbol都有同樣既magnitude就係PSK既特點 (話明PSK, 當然係用Phase 係表示訊號內容, Sine wave既振幅(Amplitude)係不變).
講左咁耐, 呢d format有咩用呢? 首先, 可以幫我地計bit rate.
每種format既symbol包含既bit數 同 symbol位置既關係:
2^(no. of bits) = no. of symbol pos.
e.g. QPSK有4個位, 咁每個symbol就代表兩個bits (00, 01, 10, 11)
如果transmitter 可以傳到25Gbd QPSK Signal(每秒25G 個symbol), 咁bit rate就係25G * 2 = 50Gb/s
如果兩條50Gb/s Signal 再Pol Mux (即係X Pol一條 QPSK, Y Pol另一條QPSK Signal; 好似光 X,Y Pol. 一邊係電 一邊係磁) 就會傳到100Gb/s
(當然要做多D工夫啦)
題外話: 你地覺得50Gb/s 多定少? 如果少, 幾多先夠?
點解Fourier transform響訊號處理方面咁重要?
我唔係樓主,不過試下提出我既睇法
好多時係frequency domain 做computation係快好多
例如計convolution如果個impulse response 好長就要好多時間計,如果轉用frequency domain計完再轉返做time domain可以更加快
另外好多時time domain signal好唔intuitive, 人腦好難理解個signal,轉左做frequency domain就容易好多睇到個signal有啲咩
Agger
比如 carrier frequency 有offset (w + delta w)
如果係receiver既角度黎睇, 佢係time domain 只會見到一餅野
係time domain compensate offset 既話要成段signal 攞出黎慢慢計
但如果做左transform, 會見到枝carrier 偏離左原本位置, 就快好多
咁點解Fourier transform 負無限in到無限
laplace transform 係0 in到無限
呢個唔識有冇數學撚答

我諗佢地一開始佢睇法唔同掛...Fourier 係將function睇成sum of sine waves
Laplace transform係轉去s-domain
都唔係frequency
Fourier transform原本係用嚟將periodic function寫成linear combination of sin and cos functions
例如你個function個period係2pi, 咁理所當然所有frequency都係整數
即係f(x) = C + a1sin(x) + a2sin(2x) + ... + b1cos(x) + ...
咁你個period越長, 咁可能出現嘅frequency就越多
就好似sin(x/100)咁
當你將個period拉到無限長(即係唔係periodic),咁你integrate曬所有野就會得到一個continuous嘅frequency spectrum
不過對於一個唔係periodic嘅function, 由負無限in到正無限其實冇乜意義
因為你咁係assume咗你個frequency domain係time-independent, 咁又邊度有signal呢?
所以你就會見到Fourier transform 通常係揀喺一個window入面做,而我地假設喺window入面個frequency domain係time-independent嘅
至於window嘅大細就取決於下面嘅balance:
window長就會 loss information
即係人地講12345,你就聽到五隻字疊曬聲,然後你唔知佢噏乜鳩咁
window太短就會 low resolution
攞調音做例子
你要ensure個誤差喺1Hz以内
咁你要做嘅野就係聽吓1秒之內有冇beat
但如果你要個誤差喺0.1Hz以内
咁你就要聽10秒(即係你個window要長10倍)
利申唔識signalling
我用maths角度睇
Window取決於source
我唔係樓主,不過試下提出我既睇法
好多時係frequency domain 做computation係快好多
例如計convolution如果個impulse response 好長就要好多時間計,如果轉用frequency domain計完再轉返做time domain可以更加快
另外好多時time domain signal好唔intuitive, 人腦好難理解個signal,轉左做frequency domain就容易好多睇到個signal有啲咩
Agger
比如 carrier frequency 有offset (w + delta w)
如果係receiver既角度黎睇, 佢係time domain 只會見到一餅野
係time domain compensate offset 既話要成段signal 攞出黎慢慢計
但如果做左transform, 會見到枝carrier 偏離左原本位置, 就快好多
咁點解Fourier transform 負無限in到無限
laplace transform 係0 in到無限
呢個唔識有冇數學撚答

我諗佢地一開始佢睇法唔同掛...Fourier 係將function睇成sum of sine waves
Laplace transform係轉去s-domain
都唔係frequency
Fourier transform原本係用嚟將periodic function寫成linear combination of sin and cos functions
例如你個function個period係2pi, 咁理所當然所有frequency都係整數
即係f(x) = C + a1sin(x) + a2sin(2x) + ... + b1cos(x) + ...
咁你個period越長, 咁可能出現嘅frequency就越多
就好似sin(x/100)咁
當你將個period拉到無限長(即係唔係periodic),咁你integrate曬所有野就會得到一個continuous嘅frequency spectrum
不過對於一個唔係periodic嘅function, 由負無限in到正無限其實冇乜意義
因為你咁係assume咗你個frequency domain係time-independent, 咁又邊度有signal呢?
所以你就會見到Fourier transform 通常係揀喺一個window入面做,而我地假設喺window入面個frequency domain係time-independent嘅
至於window嘅大細就取決於下面嘅balance:
window長就會 loss information
即係人地講12345,你就聽到五隻字疊曬聲,然後你唔知佢噏乜鳩咁
window太短就會 low resolution
攞調音做例子
你要ensure個誤差喺1Hz以内
咁你要做嘅野就係聽吓1秒之內有冇beat
但如果你要個誤差喺0.1Hz以内
咁你就要聽10秒(即係你個window要長10倍)
利申唔識signalling
我用maths角度睇
Window取決於source
講多啲?
留名學野
Modulation format
上回講左少少modulation format. 而家主流又經典既modulation format 有兩種, 一隻係QAM, 另一隻係PSK. QAM 大部分就好似上一個post d圖咁四四方方咁, 可以歸類為Square QAM (仲有長方形, 好似8QAM有8粒點)

上面一張係4 QAM, 另一張係16-QAM. 前面既數字代表呢個格式有幾多位置可以放D 點點(symbol). 但好似上一個post咁, 4 QAM係俾人叫慣QPSK, 點解呢? 因為QPSK個4點既magnitude係一樣, 而所有symbol都有同樣既magnitude就係PSK既特點 (話明PSK, 當然係用Phase 係表示訊號內容, Sine wave既振幅(Amplitude)係不變).
講左咁耐, 呢d format有咩用呢? 首先, 可以幫我地計bit rate.
每種format既symbol包含既bit數 同 symbol位置既關係:
2^(no. of bits) = no. of symbol pos.
e.g. QPSK有4個位, 咁每個symbol就代表兩個bits (00, 01, 10, 11)
如果transmitter 可以傳到25Gbd QPSK Signal(每秒25G 個symbol), 咁bit rate就係25G * 2 = 50Gb/s
如果兩條50Gb/s Signal 再Pol Mux (即係X Pol一條 QPSK, Y Pol另一條QPSK Signal; 好似光 X,Y Pol. 一邊係電 一邊係磁) 就會傳到100Gb/s
(當然要做多D工夫啦)
題外話: 你地覺得50Gb/s 多定少? 如果少, 幾多先夠?
50Gbps 單條 serdes 已經tie-1 technology


Modulation format
上回講左少少modulation format. 而家主流又經典既modulation format 有兩種, 一隻係QAM, 另一隻係PSK. QAM 大部分就好似上一個post d圖咁四四方方咁, 可以歸類為Square QAM (仲有長方形, 好似8QAM有8粒點)

上面一張係4 QAM, 另一張係16-QAM. 前面既數字代表呢個格式有幾多位置可以放D 點點(symbol). 但好似上一個post咁, 4 QAM係俾人叫慣QPSK, 點解呢? 因為QPSK個4點既magnitude係一樣, 而所有symbol都有同樣既magnitude就係PSK既特點 (話明PSK, 當然係用Phase 係表示訊號內容, Sine wave既振幅(Amplitude)係不變).
講左咁耐, 呢d format有咩用呢? 首先, 可以幫我地計bit rate.
每種format既symbol包含既bit數 同 symbol位置既關係:
2^(no. of bits) = no. of symbol pos.
e.g. QPSK有4個位, 咁每個symbol就代表兩個bits (00, 01, 10, 11)
如果transmitter 可以傳到25Gbd QPSK Signal(每秒25G 個symbol), 咁bit rate就係25G * 2 = 50Gb/s
如果兩條50Gb/s Signal 再Pol Mux (即係X Pol一條 QPSK, Y Pol另一條QPSK Signal; 好似光 X,Y Pol. 一邊係電 一邊係磁) 就會傳到100Gb/s
(當然要做多D工夫啦)
題外話: 你地覺得50Gb/s 多定少? 如果少, 幾多先夠?
50Gbps 單條 serdes 已經tie-1 technology
係DAC的錯
其實而家bit rate supply 已經meet 唔到demand
 無野可以多講)
無野可以多講)Modulation format
上回講左少少modulation format. 而家主流又經典既modulation format 有兩種, 一隻係QAM, 另一隻係PSK. QAM 大部分就好似上一個post d圖咁四四方方咁, 可以歸類為Square QAM (仲有長方形, 好似8QAM有8粒點)

上面一張係4 QAM, 另一張係16-QAM. 前面既數字代表呢個格式有幾多位置可以放D 點點(symbol). 但好似上一個post咁, 4 QAM係俾人叫慣QPSK, 點解呢? 因為QPSK個4點既magnitude係一樣, 而所有symbol都有同樣既magnitude就係PSK既特點 (話明PSK, 當然係用Phase 係表示訊號內容, Sine wave既振幅(Amplitude)係不變).
講左咁耐, 呢d format有咩用呢? 首先, 可以幫我地計bit rate.
每種format既symbol包含既bit數 同 symbol位置既關係:
2^(no. of bits) = no. of symbol pos.
e.g. QPSK有4個位, 咁每個symbol就代表兩個bits (00, 01, 10, 11)
如果transmitter 可以傳到25Gbd QPSK Signal(每秒25G 個symbol), 咁bit rate就係25G * 2 = 50Gb/s
如果兩條50Gb/s Signal 再Pol Mux (即係X Pol一條 QPSK, Y Pol另一條QPSK Signal; 好似光 X,Y Pol. 一邊係電 一邊係磁) 就會傳到100Gb/s
(當然要做多D工夫啦)
題外話: 你地覺得50Gb/s 多定少? 如果少, 幾多先夠?
50Gbps 單條 serdes 已經tie-1 technology
係DAC的錯
其實而家bit rate supply 已經meet 唔到demand
DAC要睇 bit數
(btw 我唔係個範無野可以多講)

我唔係樓主,不過試下提出我既睇法
好多時係frequency domain 做computation係快好多
例如計convolution如果個impulse response 好長就要好多時間計,如果轉用frequency domain計完再轉返做time domain可以更加快
另外好多時time domain signal好唔intuitive, 人腦好難理解個signal,轉左做frequency domain就容易好多睇到個signal有啲咩
Agger
比如 carrier frequency 有offset (w + delta w)
如果係receiver既角度黎睇, 佢係time domain 只會見到一餅野
係time domain compensate offset 既話要成段signal 攞出黎慢慢計
但如果做左transform, 會見到枝carrier 偏離左原本位置, 就快好多
咁點解Fourier transform 負無限in到無限
laplace transform 係0 in到無限
呢個唔識有冇數學撚答

我諗佢地一開始佢睇法唔同掛...Fourier 係將function睇成sum of sine waves
Laplace transform係轉去s-domain
都唔係frequency
Fourier transform原本係用嚟將periodic function寫成linear combination of sin and cos functions
例如你個function個period係2pi, 咁理所當然所有frequency都係整數
即係f(x) = C + a1sin(x) + a2sin(2x) + ... + b1cos(x) + ...
咁你個period越長, 咁可能出現嘅frequency就越多
就好似sin(x/100)咁
當你將個period拉到無限長(即係唔係periodic),咁你integrate曬所有野就會得到一個continuous嘅frequency spectrum
不過對於一個唔係periodic嘅function, 由負無限in到正無限其實冇乜意義
因為你咁係assume咗你個frequency domain係time-independent, 咁又邊度有signal呢?
所以你就會見到Fourier transform 通常係揀喺一個window入面做,而我地假設喺window入面個frequency domain係time-independent嘅
至於window嘅大細就取決於下面嘅balance:
window長就會 loss information
即係人地講12345,你就聽到五隻字疊曬聲,然後你唔知佢噏乜鳩咁
window太短就會 low resolution
攞調音做例子
你要ensure個誤差喺1Hz以内
咁你要做嘅野就係聽吓1秒之內有冇beat
但如果你要個誤差喺0.1Hz以内
咁你就要聽10秒(即係你個window要長10倍)
利申唔識signalling
我用maths角度睇
Window取決於source
講多啲?
留名學野
講下 Fourier transform
practical來說用 DFT 多
講 DFT好過
