點解Fourier transform響訊號處理方面咁重要？
我唔係樓主，不過試下提出我既睇法
好多時係frequency domain 做computation係快好多
例如計convolution如果個impulse response 好長就要好多時間計，如果轉用frequency domain計完再轉返做time domain可以更加快
另外好多時time domain signal好唔intuitive, 人腦好難理解個signal,轉左做frequency domain就容易好多睇到個signal有啲咩
Agger
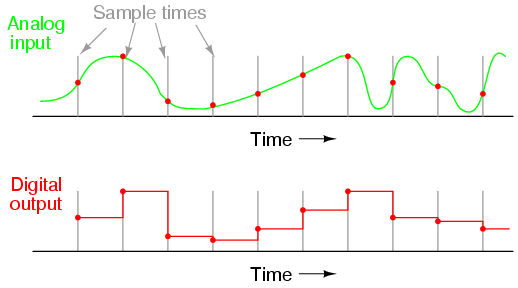
比如 carrier frequency 有offset (w + delta w)
如果係receiver既角度黎睇, 佢係time domain 只會見到一餅野
係time domain compensate offset 既話要成段signal 攞出黎慢慢計
但如果做左transform, 會見到枝carrier 偏離左原本位置, 就快好多
咁點解Fourier transform 負無限in到無限
laplace transform 係0 in到無限
呢個唔識
有冇數學撚答
我諗佢地一開始佢睇法唔同掛...Fourier 係將function睇成sum of sine waves
Laplace transform係轉去s-domain
都唔係frequency
Fourier transform原本係用嚟將periodic function寫成linear combination of sin and cos functions
例如你個function個period係2pi, 咁理所當然所有frequency都係整數
即係f(x) = C + a1sin(x) + a2sin(2x) + ... + b1cos(x) + ...
咁你個period越長, 咁可能出現嘅frequency就越多
就好似sin(x/100)咁
當你將個period拉到無限長(即係唔係periodic
),咁你integrate曬所有野就會得到一個continuous嘅frequency spectrum
不過對於一個唔係periodic嘅function, 由負無限in到正無限其實冇乜意義
因為你咁係assume咗你個frequency domain係time-independent, 咁又邊度有signal呢?
所以你就會見到Fourier transform 通常係揀喺一個window入面做,而我地假設喺window入面個frequency domain係time-independent嘅
至於window嘅大細就取決於下面嘅balance:
window長就會 loss information
即係人地講12345,你就聽到五隻字疊曬聲,然後你唔知佢噏乜鳩咁
window太短就會 low resolution
攞調音做例子
你要ensure個誤差喺1Hz以内
咁你要做嘅野就係聽吓1秒之內有冇beat
但如果你要個誤差喺0.1Hz以内
咁你就要聽10秒(即係你個window要長10倍)
利申唔識signalling
我用maths角度睇
