一般媒體的報導多半僅止於此,並不是!其實還有一個重點是如何扭轉這個「萬事天注定」的宿命論,讓具有才能的人出頭天。
他們的研究是利用「代理人模型」(agent-based model),也就是模型中的基本單元就是一個一個虛擬世界中的人,然後根據研究的問題「假設」來制訂行動規則,接著就讓這些「代理人」依照規則行動,看看結果如何。如果模擬出來的結果符合我們看到的社會現象,那麼上述的「假設」就可能為真。
在這個「TvL 模型」(Talent vs Luck, 天才對運氣)中有 1000 個代理人,他們被隨機灑在一個 201×201 的方格棋盤上面,每個人佔據一個空格,每個人身上帶著 10 塊錢——這裡我們姑且用金錢來衡量「成功的程度」,它也可以是在政治界官位的高度、學術界發表論文的數量與影響力……等其他面向量化後的「成就點數」。
接著同樣在這個棋盤上面隨機灑出一些綠色跟紅色的點,它們代表「人生中可能會遇到的事件」,綠色代表「幸運事件」,紅色代表「不幸事件」。事件的總數是人數的一半,也就是 500 個,其中紅綠各有 250 個。

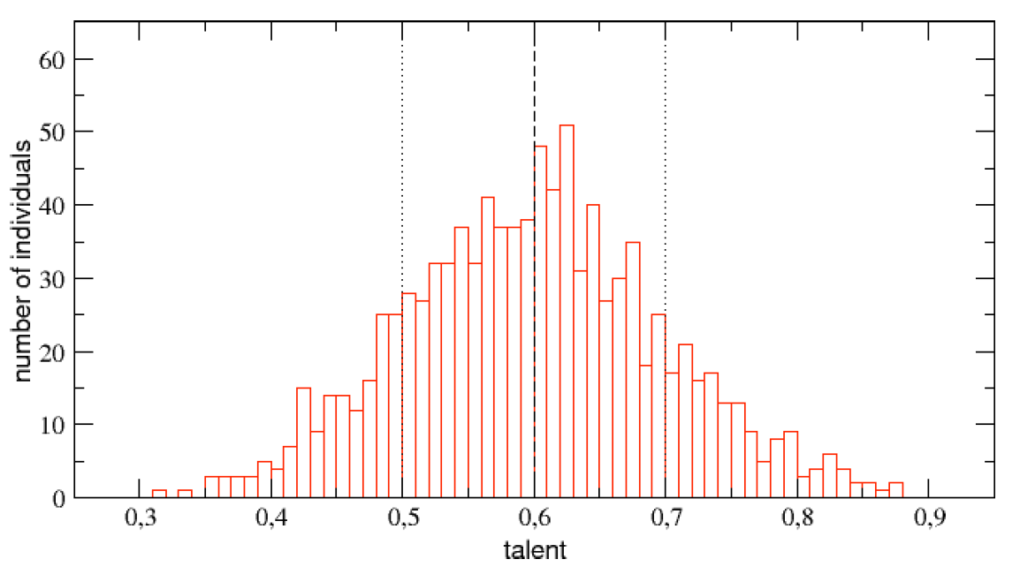
假設每個人的「才能」是標準化後,介於 0 到 1 之間的常態分布,平均值為 0.6,標準差為 0.1。這裡用單一的變數 T 來代表才能,它包含了智商、個性、努力、教育……等出道前養成的所有個人屬性。
這個世界變化的規則如下:
「人」不會動,從頭到尾待在原地。
每一步中,每個「事件」會任選一個方向,移動兩格。
如果某個人剛好在某個事件移動的路徑上(直接撞到)、或者是與路徑相鄰(擦身而過),表示他身上「出事了」。
如果碰到的是綠點,表示「好事發生」。不過「運氣屬於準備好的人」,手裡錢(或成就點數)有機會翻倍,發生的機率就是才能值 T。所以才能較高的人,比較能掌握幸運的機會。
如果碰到的是紅點,表示「發生不幸」,跟幸運不一樣的是:「不幸」是公平的,遇上的人金錢一律減半。這個設定的基礎是這樣:不管上智或下愚,路上被車撞就是得送醫、住院;被地震颱風直接命中就是會變成受災戶,你有再高的才能也無用武之地。
沒有被事件撞到或擦到的人,金錢不變。
回到 1。
假設每個人從菜鳥出道一直到退休一共奮鬥 40 年,而每半年就可能碰到一次重大的事件,所以整個模型需要模擬的就是每半年一次的變化,一共 80 步後,遊戲結束,來計算一下成績,最後大家手裡有多少錢呢?
結果顯示經過一生的努力後,財富分布滿足大家熟悉的「80-20」法則,前 20% 的人擁有整個社會 80% 的財富。雖然「80-20 法則」通常是拿來批評「貧富不均」這個社會現象,其實它有更深一層的涵意:如果只看前 20% 的有錢人,就會發現這裡面的 20% 也一樣會擁有其中 80% 的財富!也就是「有錢人之間」也是有「貧富不均」的現象。換算一下可以得知,前 4% 的有錢人(前 20% 的前 20%)擁有整個社會 64% 的財富(80% 的 80%);然後再看最有錢的前 4% 的「超有錢俱樂部」中,同樣符合「80-20 法則」!
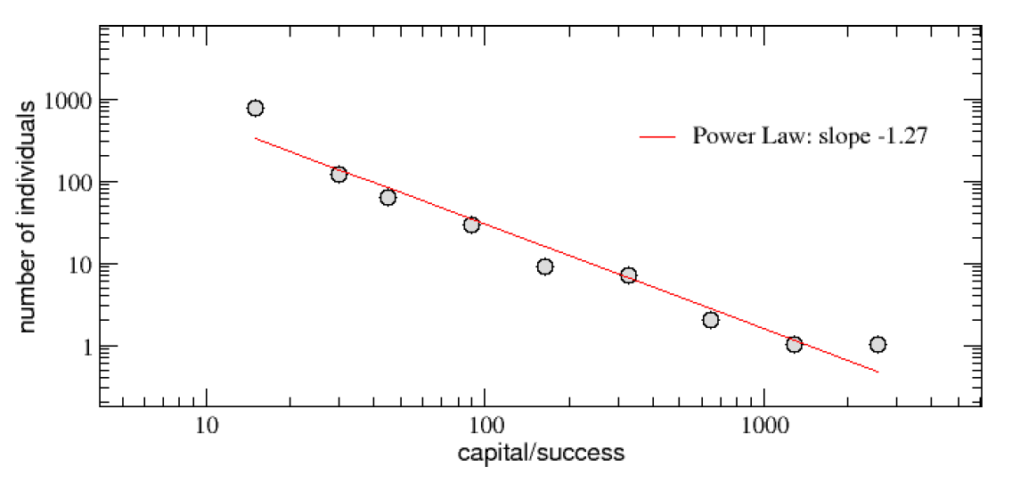
目前人類社會的財富分布,就符合這個奇妙的法則,在數學上,「財富數量」與「擁有這個數量的人數比例」會呈現「冪次律」(power law)特性,兩邊都取對數做成圖的話,會呈現一直線。
這個超級簡單的 TvL 模型到底能不能反應真實世界的狀況?由圖三看起來,它的確能重現財富分配「80-20 法則」的「冪次律」特性,所以模型雖然簡單,的確有抓到財富分布最重要的特性,也讓後面的結果具有說服力。
那麼,誰是這場遊戲的第一名?
因為人的位置跟事件的移動都是隨機、公平的,而才能高的人抓住幸運事件讓錢倍增的機率較高,所以最後的贏家應該是才能很高的傢伙吧?
很合理的想法,不過結果可能會讓你吃一驚:第一名的才能 T=0.61,非常接近平均值,他最後手上有 2560 元,成長了 256 倍;而最慘的人居然擁有 T=0.74 的才能,以常態分布來說,是排名在前 7%,或是 PR93 的強者。如果覺得只看第一名跟最後一名不準的話,就來看看所有人的成績分布吧!
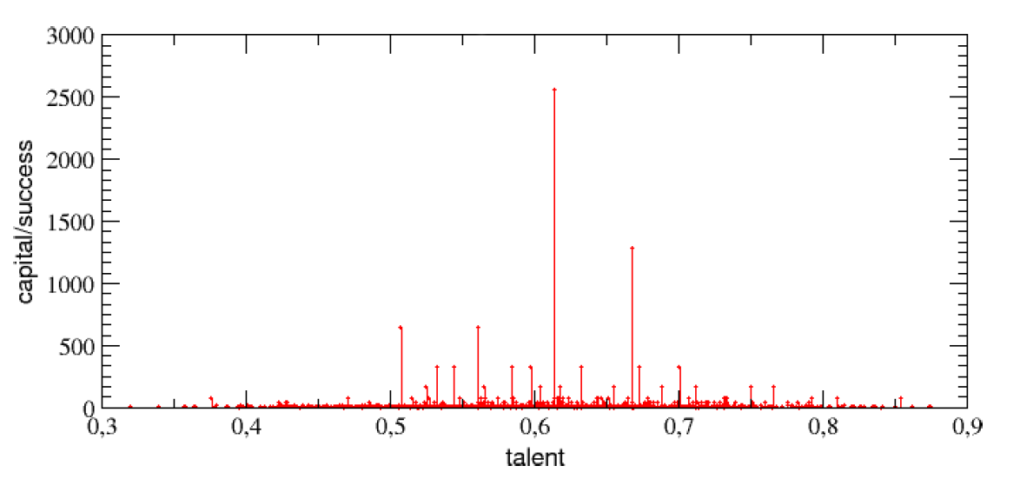
從圖四可以看出來,以最高的 T=0.61 那一點為中心,左右兩邊大體上是對稱的。看起來,才能高的人,真的好像不見得在這個「人生遊戲」終站到便宜!
那到底你將成為「人生勝利組」或是「魯蛇」,決定性的因素到底是什麼?答案是「運氣」。
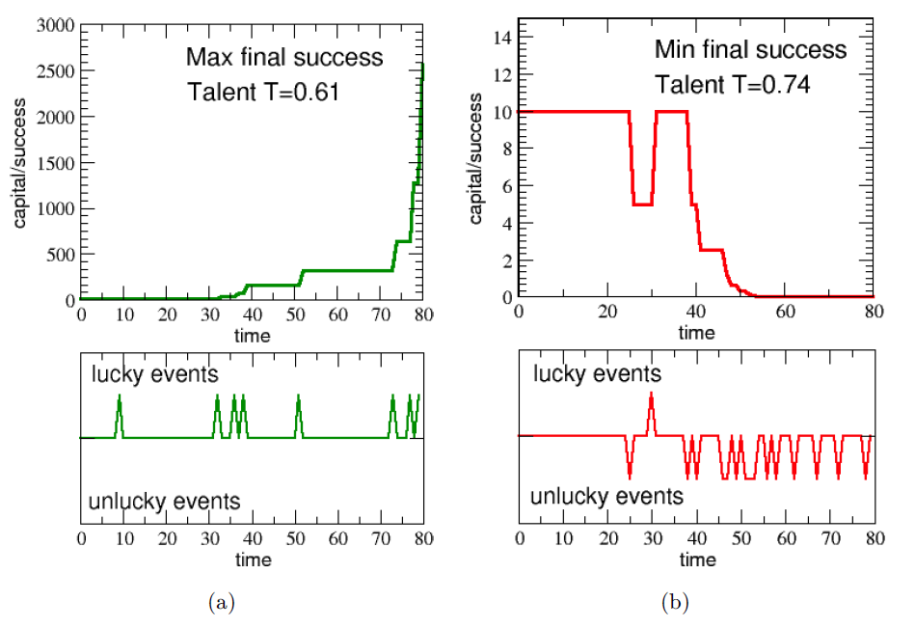
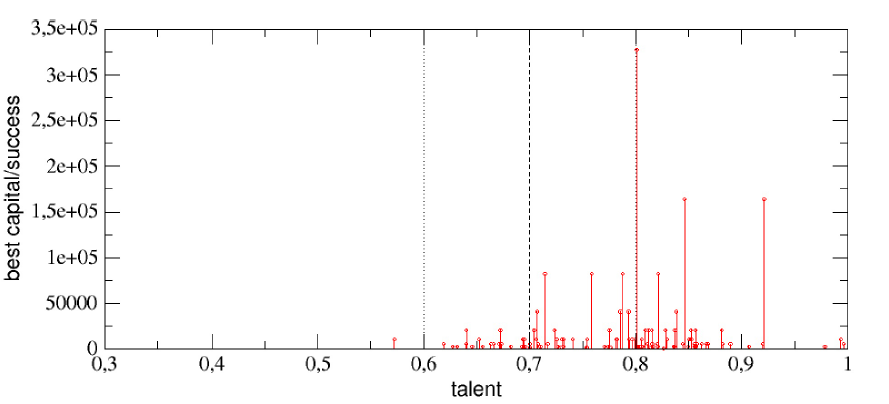
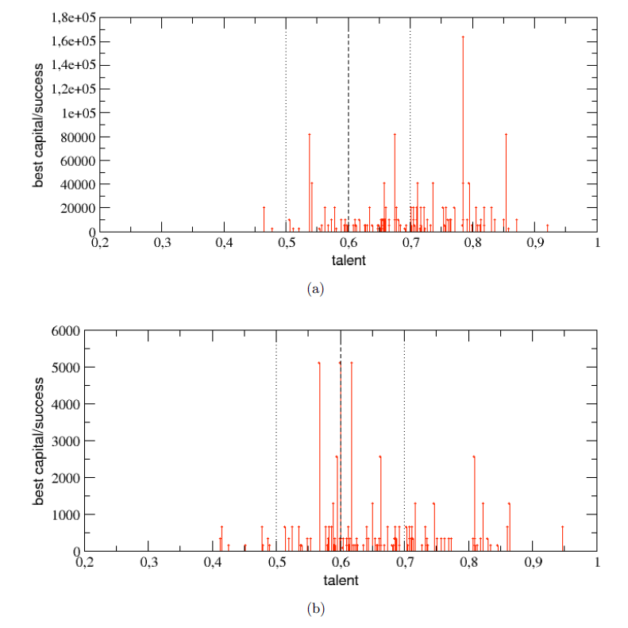
就算資質平庸,抓住好運的機率稍微差一點,只要你在人生的過程中,碰上好事的機率比別人多很多,你還是可能出人頭地,成為頂尖人物。圖五清楚的顯示了這兩個人的運氣差多少:(a)第一名的人生,發生了八次幸運事件,而且雖然機率只有 61%,很幸運的也每次都掌握到了,而厄運則是一次也沒有!(b)反觀最後一名的人生,厄運連連高達 15 次,而且根據模型規則,毫無招架之力一次也躲不掉!好事只有發生一次,真想幫他寫個「慘」字……。
這只是一次的模擬,有可能只是湊巧出現這種令人意外的結果。別擔心,物理學家雖然頭腦簡單,做事情挺小心的,模擬個 100 次吧!然後看看每次的第一名的人的才能值的分布狀況,發現才能還是有差啦!但是並沒有很戲劇性的差別。拿到各次模擬第一名的人,平均才能值是 0.66,比起平均值 0.6 稍大一些,大概是「均標以上、前標未滿」的程度。100 次不夠,來個 10000 次吧!等於是 1000 萬個人生,得出來的結果差不多,10000 個「第一名」的平均才能是 0.667(圖六)。
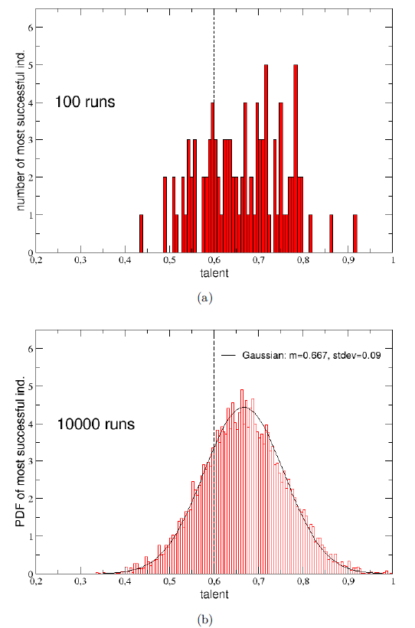
看起來,才能高低對最後的結果是會有影響,但是頗為有限,運氣的影響大很多。而且,檢視才能比平均人高出一個標準差以上,也就是 T > 0.7,或是 PR84 以上的「秀才」,他們的成功率如何呢?這裡「成功」的定亦是,只要你在工作 40 年後,手上的錢不少於剛出道時(10 元)就可以了。天啊這標準也太低,不過在這種低標準之下,這些秀才的成功率也只有 32.05% 而已!人生真的好難!
看到這裡不禁覺得充滿負能量,大家都別再努力了,反正運氣決定一切……。
作者接著問,現實如此殘酷,政府能為我們做些什麼?
政府在挹注資源扶植科技研發、經濟產業等領域時,經常會有一種「菁英主義」思維:「我們如果把資源集中投給那些有才能的人,應該能夠得到更好的效果吧!」不過「才能」很難一下子看得出來,所以就變成「有才能的人應該本來就會表現得比一般人好,那就把資源給那些過去表現比較好的人吧!」
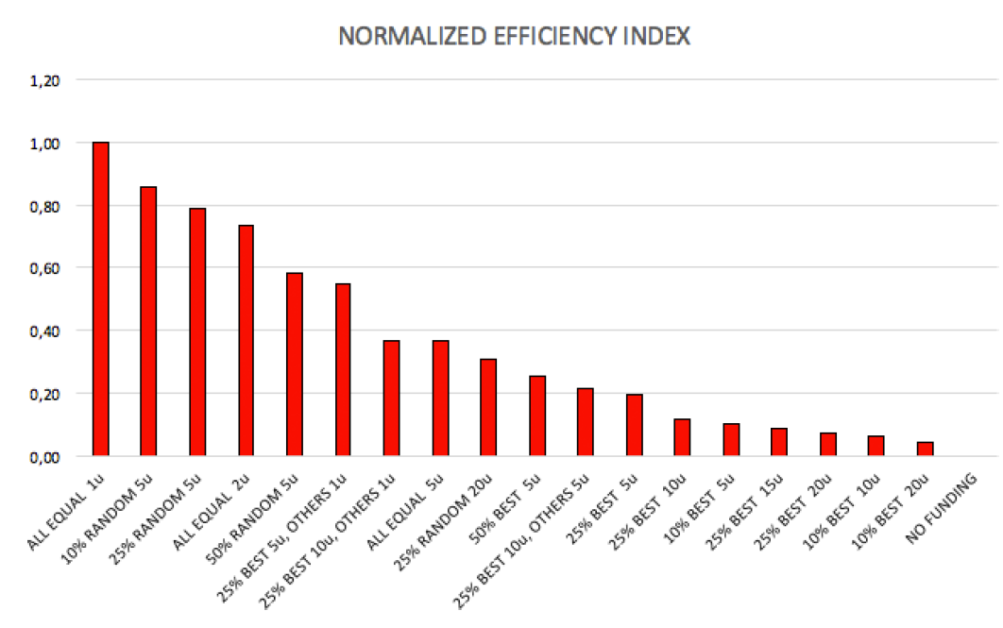


 精英主義係差過以上三個方案
精英主義係差過以上三個方案