有冇思考過擲彩虹呢個遊戲有冇技術含量?
外賣步兵羅翰霆
280 回覆
166 Like
29 Dislike
好耐冇聽過呢個 term ,清文化人
細個係黃埔間namco,掉中左兩部數碼暴龍機,基本上有一部係職員送咁濟
主要係睇職員





銀仔下面果層玻璃, 所以側邊睇睇到黃色, 垂直睇係擲界.
收一個銀有一蚊花紅 送禮出去要員工自付
有個啲公仔都係百令蚊隻 驗屍咁驗 真係反社會人格
我覺得要裝個VAR係到
有無一路打一路係到笑?






兩邊到有黃色喎 ching
有 好好笑
好好笑
 好好笑
好好笑之前有講過 因為個圖案面係有塊膠片
如果斜望 唔同角度會有影響
如果斜望 唔同角度會有影響
原文﹕
http://elvissharing.blogspot.com/2022/02/misc-bs.html

假設掟代幣呢件事係完全隨機事件。[我唔認為掟彩虹可以有技術可言,因為只要以下任何一個因素有極少嘅誤差,如出手力度、角度變化、或代幣相對水平面嘅角度、空氣阻力、代幣以自由落體跌落枱面時之角度及力度、代幣於枱面滑行時之摩擦力等等,就可以做成完全無法預測嘅結果,咁多不確定因素綜合一齊的話,唔係話苦練就可以掌握;唔似得掟飛鏢,飛鏢係有較重嘅鏢身及鏢翼力穩定飛行軌迹及排除大部份嘅空氣阻力干擾因素,可以用眼、手、鏢、紅心等拉一直線以瞄準,兼且唔需要考慮命中目標後嘅角度、力度及滑行一斷時間所做成嘅一系列不確定因素。所以我認為,掟飛鏢係有得練,但掟彩虹係冇得練。]
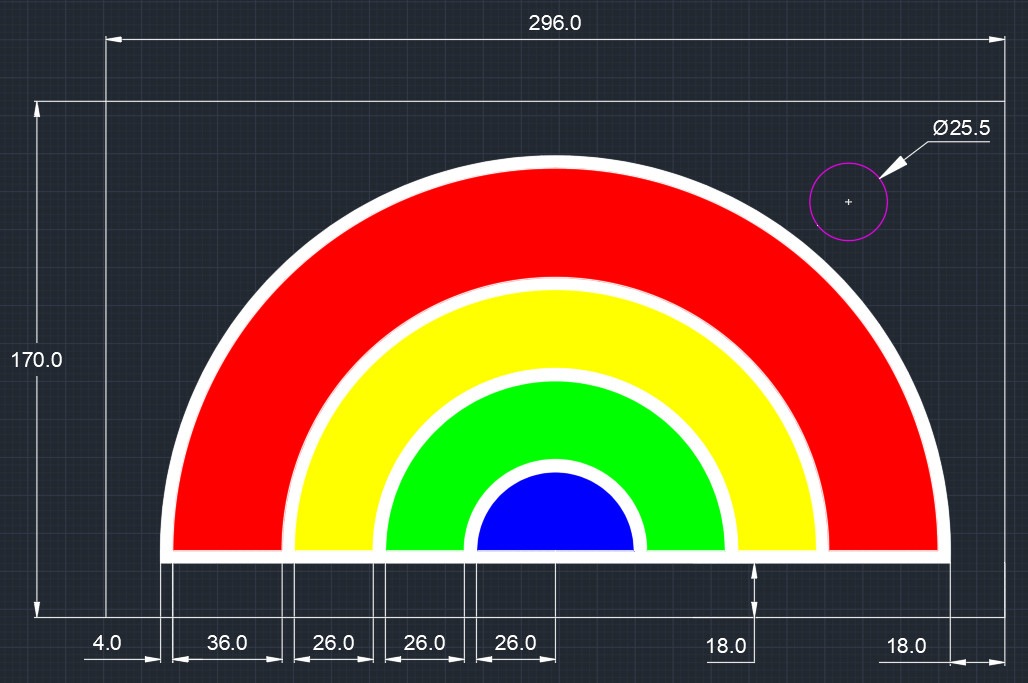
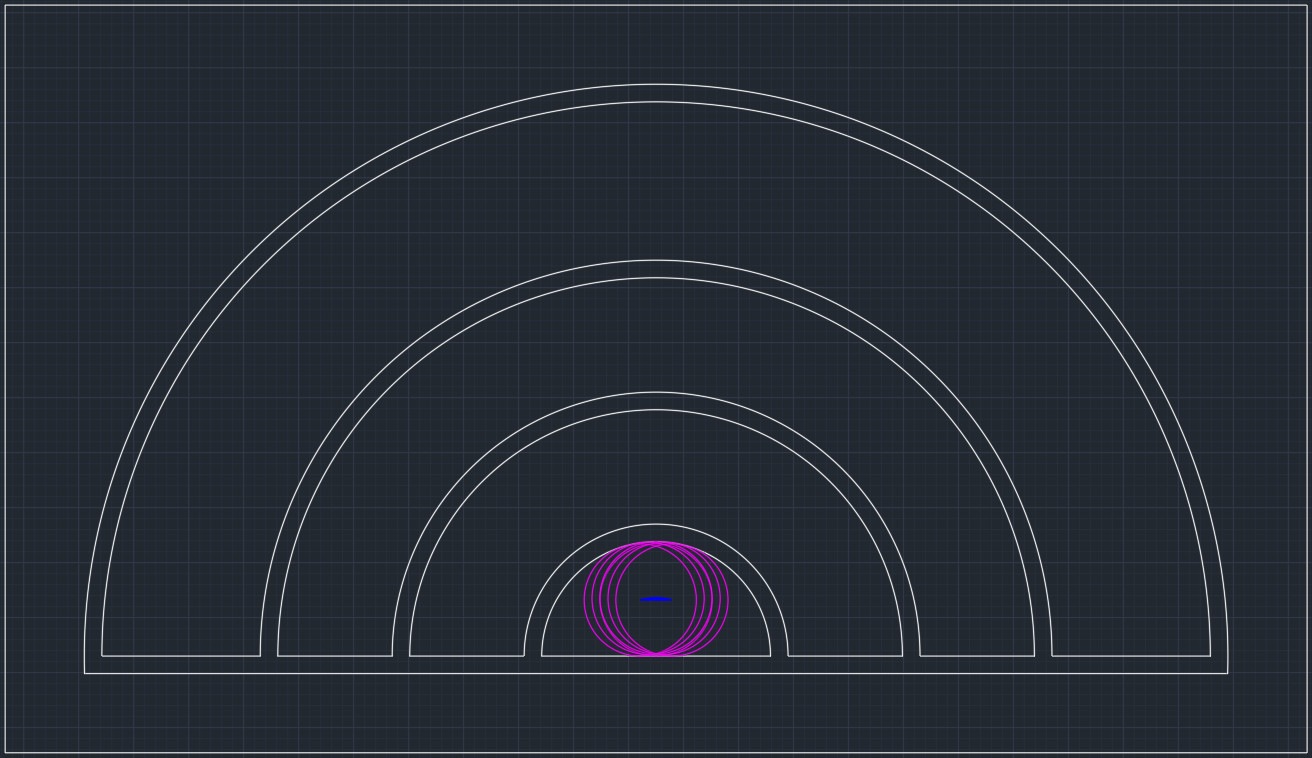
首先,將上圖拍入個CAD軟件,勾返啲線出嚟同埋scale返個比例,如下圖﹕

跟住拉返啲呎吋,再用CAD計算一紅、黃、綠、藍及空白部份嘅面積﹕
我地先睇黃色部份中獎概率係幾多﹕
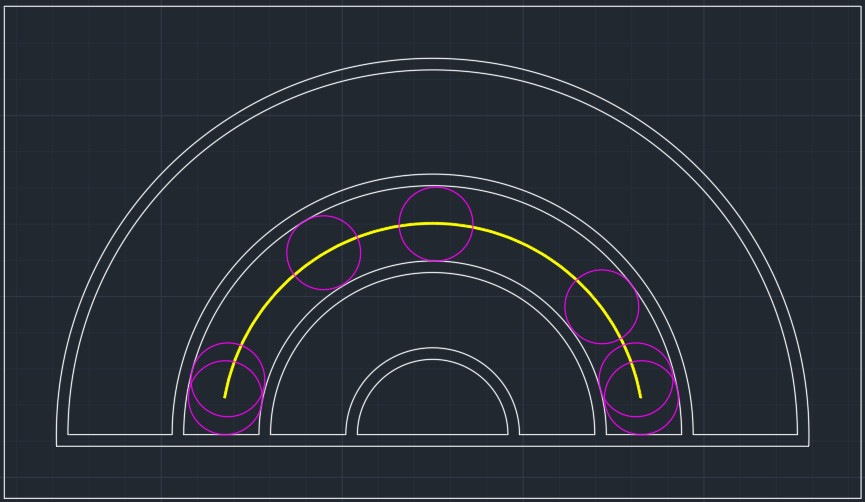
只有個硬幣嘅圓心响黃色嘅位置先至叫中獎。
而我地又有以下嘅公式﹕
期望值=概率x回報
舉個例子,有一隻擲一粒骰仔嘅遊戲,擲中六點就有獎,擲到一至五點都冇獎,每次落注係$10, 咁個獎品要值幾錢呢隻遊戲先值得玩?
期望值($10)=概率(1/6)x回報
回報起碼要有$60先值得玩呢隻遊戲
用CAD我地可以計算到,黃色部份嘅面積大概係100.27; 設一個代幣係HKD$1.0; 整個彩虹區域嘅面積係50320;
$1.0=100.27/50320*回報=$502
即係如果你想中黃色區域嘅獎品,除非回報比你嗰件獎品價值高過$502, 否則呢隻遊戲係玩唔過;
再睇下綠色區域﹕
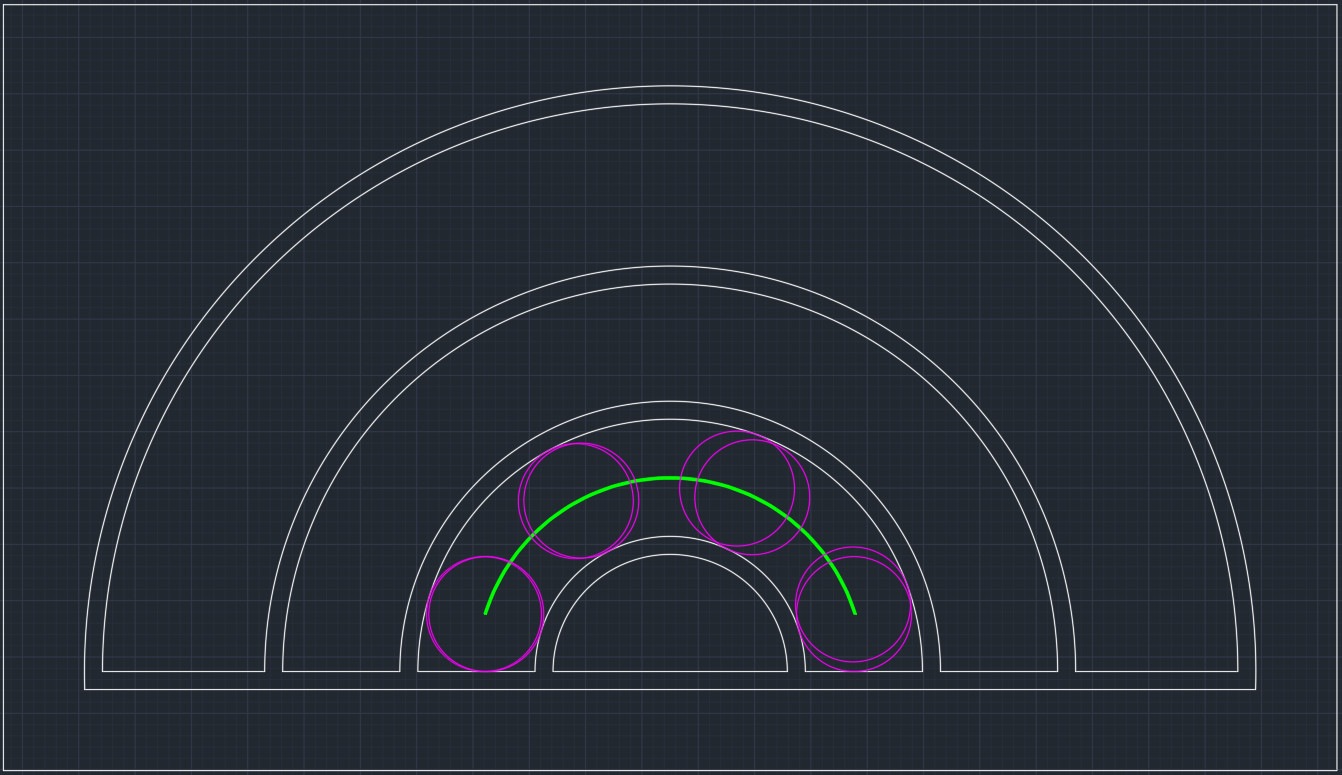
$1.0=52.14/50320*回報=$965
即係如果你想中綠色區域嘅獎品,除非回報比你嗰件獎品價值高過$965, 否則呢隻遊戲係玩唔過;
再睇下紅色區域﹕
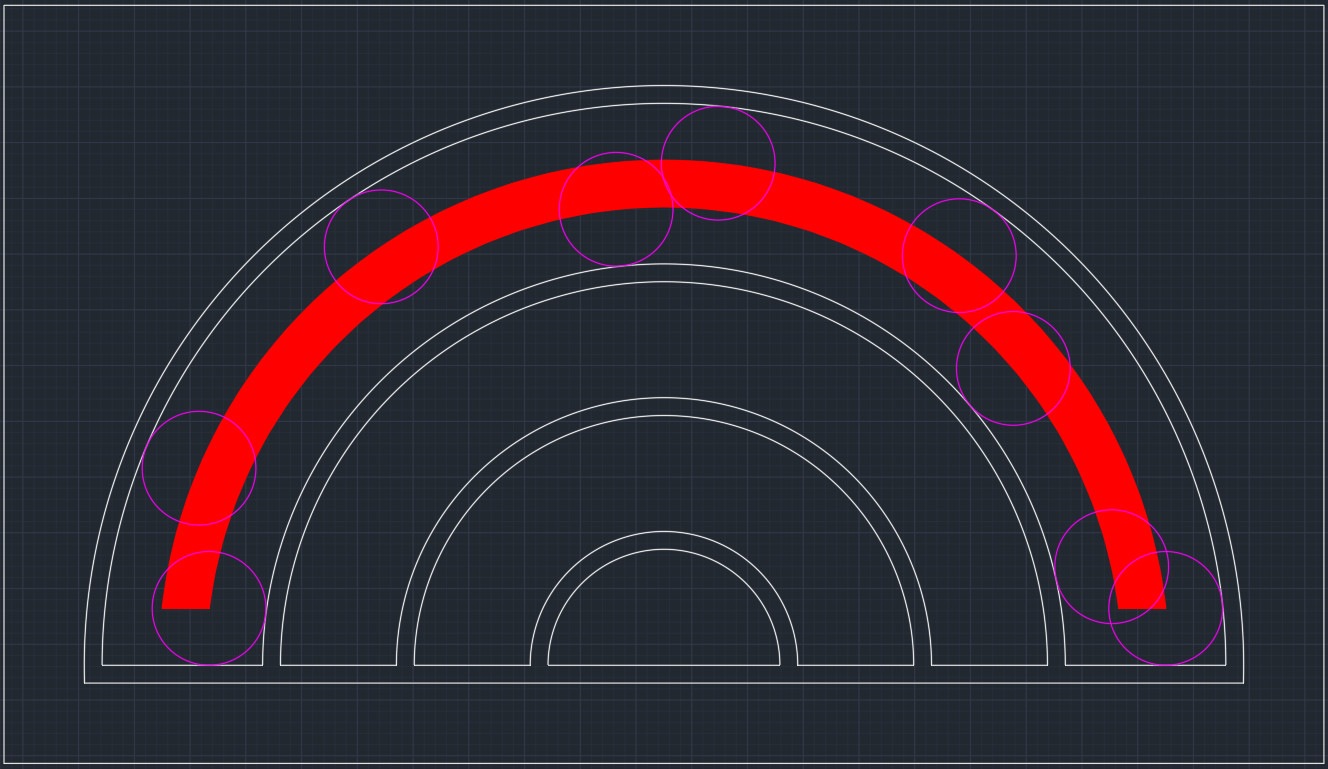
$1.0=3271.85/50320*回報=$15.4
即係如果你想中紅色區域嘅獎品,除非回報比你嗰件獎品價值高過$15.4, 否則呢隻遊戲係玩唔過;
*要留意嘅係,假設簡化咗中紅色區域個概率係1/15, 但並不等於你掟15次就保證你可以中一次。可以用一個網上probability calculator裡面嘅"probability of a series of independent events", 响Event A輸入probability: 1/15=0.66667; repeat times=15, event b可ignore, 然後按calculate, 可以見到probability of A NOT occuring即係掟15次一次都唔中嘅概率係有35.5%
再睇埋終極大獎嘅藍色區域﹕
$1.0=2.4221/50320*回報=$20775
即係如果你想中綠色區域嘅獎品,除非回報比你嗰件獎品價值高過$20775, 否則呢隻遊戲係玩唔過;
呢個只係BS人用嘅簡單而粗暴計算方法,一定唔係最好最聰明做法,還望有數學/programme高手提出更好嘅做法。
再睇返第一張圖嘅藍色/綠色區域獎品,值唔值$20775或$965就見仁見智。當然上述未計明明擲中冇責界職員唔認數等因數。
http://elvissharing.blogspot.com/2022/02/misc-bs.html

假設掟代幣呢件事係完全隨機事件。[我唔認為掟彩虹可以有技術可言,因為只要以下任何一個因素有極少嘅誤差,如出手力度、角度變化、或代幣相對水平面嘅角度、空氣阻力、代幣以自由落體跌落枱面時之角度及力度、代幣於枱面滑行時之摩擦力等等,就可以做成完全無法預測嘅結果,咁多不確定因素綜合一齊的話,唔係話苦練就可以掌握;唔似得掟飛鏢,飛鏢係有較重嘅鏢身及鏢翼力穩定飛行軌迹及排除大部份嘅空氣阻力干擾因素,可以用眼、手、鏢、紅心等拉一直線以瞄準,兼且唔需要考慮命中目標後嘅角度、力度及滑行一斷時間所做成嘅一系列不確定因素。所以我認為,掟飛鏢係有得練,但掟彩虹係冇得練。]
首先,將上圖拍入個CAD軟件,勾返啲線出嚟同埋scale返個比例,如下圖﹕

跟住拉返啲呎吋,再用CAD計算一紅、黃、綠、藍及空白部份嘅面積﹕

我地先睇黃色部份中獎概率係幾多﹕

只有個硬幣嘅圓心响黃色嘅位置先至叫中獎。
而我地又有以下嘅公式﹕
期望值=概率x回報
舉個例子,有一隻擲一粒骰仔嘅遊戲,擲中六點就有獎,擲到一至五點都冇獎,每次落注係$10, 咁個獎品要值幾錢呢隻遊戲先值得玩?
期望值($10)=概率(1/6)x回報
回報起碼要有$60先值得玩呢隻遊戲
用CAD我地可以計算到,黃色部份嘅面積大概係100.27; 設一個代幣係HKD$1.0; 整個彩虹區域嘅面積係50320;
$1.0=100.27/50320*回報=$502
即係如果你想中黃色區域嘅獎品,除非回報比你嗰件獎品價值高過$502, 否則呢隻遊戲係玩唔過;
再睇下綠色區域﹕

$1.0=52.14/50320*回報=$965
即係如果你想中綠色區域嘅獎品,除非回報比你嗰件獎品價值高過$965, 否則呢隻遊戲係玩唔過;
再睇下紅色區域﹕

$1.0=3271.85/50320*回報=$15.4
即係如果你想中紅色區域嘅獎品,除非回報比你嗰件獎品價值高過$15.4, 否則呢隻遊戲係玩唔過;
*要留意嘅係,假設簡化咗中紅色區域個概率係1/15, 但並不等於你掟15次就保證你可以中一次。可以用一個網上probability calculator裡面嘅"probability of a series of independent events", 响Event A輸入probability: 1/15=0.66667; repeat times=15, event b可ignore, 然後按calculate, 可以見到probability of A NOT occuring即係掟15次一次都唔中嘅概率係有35.5%
再睇埋終極大獎嘅藍色區域﹕

$1.0=2.4221/50320*回報=$20775
即係如果你想中綠色區域嘅獎品,除非回報比你嗰件獎品價值高過$20775, 否則呢隻遊戲係玩唔過;
呢個只係BS人用嘅簡單而粗暴計算方法,一定唔係最好最聰明做法,還望有數學/programme高手提出更好嘅做法。
再睇返第一張圖嘅藍色/綠色區域獎品,值唔值$20775或$965就見仁見智。當然上述未計明明擲中冇責界職員唔認數等因數。
VAR!!!!


係咪都會好多人玩㗎啦
咪傻
咪傻
經理又唔係有佣分 梗係唔想咁多人黎玩

藍色擲底界
無 同兩個friend 玩過 每人十個銀
同兩個friend 玩過 每人十個銀
我鳩掟佢哋認真掟,完全無諗過中
最後我中到中間同細嗰兩格 佢哋得大格
佢哋得大格
 同兩個friend 玩過 每人十個銀
同兩個friend 玩過 每人十個銀我鳩掟佢哋認真掟,完全無諗過中

最後我中到中間同細嗰兩格
 佢哋得大格
佢哋得大格
張枱係有塊膠放面先到彩虹圖案
所以打斜同垂直係會睇到有分別
所以打斜同垂直係會睇到有分別
幾百個會唔會太勁

專搵d 少員工少人玩既位, 然後左一個右一個咁拋

見#113 分析
簡單結論,就算職員唔搵笨實都好,掟彩虹呢隻遊戲都絕對玩唔過純屬智商稅。如果你嘅小朋友想玩,可以趁呢個機會教埋佢地基本概率。
簡單結論,就算職員唔搵笨實都好,掟彩虹呢隻遊戲都絕對玩唔過純屬智商稅。如果你嘅小朋友想玩,可以趁呢個機會教埋佢地基本概率。
有次同幾個朋友去玩
其中一個痴線醉酒佬 用個銀仔掉個靚仔員工
之後話 咁係咪贏咗你
其中一個痴線醉酒佬 用個銀仔掉個靚仔員工
之後話 咁係咪贏咗你
