
點解擲同一塊銀仔10次 擲到5次公既期望值係50%?
EQless
35 回覆
2 Like
18 Dislike

一係公一係字
咁咪50 50囉
期望係咁架啦 實際唔係呀嘛
香港女多過男 期望值係人人有女
咁咪50 50囉
期望係咁架啦 實際唔係呀嘛
香港女多過男 期望值係人人有女
因為每一次嘅概率係獨立,唔係連續
因為你計錯
你statement錯
咁點解啲初生嬰兒唔係男就女嘅

因為中公同中字嘅機率一樣
唔會又唔中公又唔中字棟咗喺到
咁咪5050囉
唔會又唔中公又唔中字棟咗喺到
咁咪5050囉
個或然率仲低過0啊
知唔知乜撚野叫期望值呀?
我都淨係諗到少林足球
人人期望可達到

樓主係我表弟
佢有中度弱智
大家比條生路佢
佢仲服用緊精神科藥物
佢有中度弱智
大家比條生路佢
佢仲服用緊精神科藥物
擲同一塊銀仔10次,擲到5次公既機會率係24.61%
PS: 亂答,唔知樓主講緊乜
PS: 亂答,唔知樓主講緊乜
樓主 D 語言邏輯亂到
係擲到公次數嘅期望值係 5

係擲到公次數嘅期望值係 5

將每次擲銀仔當成一個 Bernoulli trial,當中擲到公嘅機率係 50%。
呢個 Bernoulli trial 會重複 10 次,而喺呢 10 次入面擲到公嘅公嘅次數 X 就係一個 binomial random variable,當中 X = 0, 1, 2, 3, ..., 10
計 x 次公機率嘅公式係呢條

括號入面嘅 n x 其實係 nCr 嘅另一個寫法,即係 n 個入面抽 x 個有幾多 combination。
呢如計 P(X = 5) = 10C5 * 0.5^5 * 0.5*5 = 0.2461
上面已經有巴打計到
另一個計法係用返中學嘅 concept
Total sample space 有 2^10 = 1024 個 combinations
擲中 5 公 5 字嘅 combinations 係 10! / (5!5!) = 252
所以 P(X = 5) = 252 / 1024 = 0.2461
如果將所有 P(X=0) P(X=1) ... P(X=10) 計晒出嚟 plot 喺幅 graph 度會得到一幅 binomial distribution。
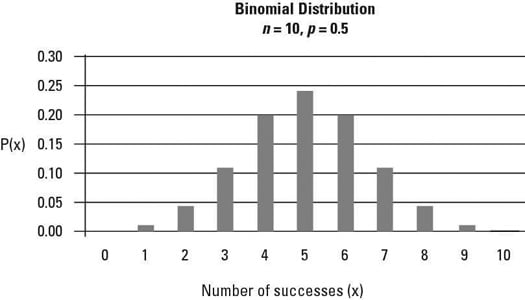
而期望值,或者叫平均值,喺呢度講緊嘅係擲中公嘅次數,亦即係 10 * 0.5 = 5 次。
呢個 Bernoulli trial 會重複 10 次,而喺呢 10 次入面擲到公嘅公嘅次數 X 就係一個 binomial random variable,當中 X = 0, 1, 2, 3, ..., 10
計 x 次公機率嘅公式係呢條

括號入面嘅 n x 其實係 nCr 嘅另一個寫法,即係 n 個入面抽 x 個有幾多 combination。
呢如計 P(X = 5) = 10C5 * 0.5^5 * 0.5*5 = 0.2461

上面已經有巴打計到
另一個計法係用返中學嘅 concept
Total sample space 有 2^10 = 1024 個 combinations
擲中 5 公 5 字嘅 combinations 係 10! / (5!5!) = 252
所以 P(X = 5) = 252 / 1024 = 0.2461
如果將所有 P(X=0) P(X=1) ... P(X=10) 計晒出嚟 plot 喺幅 graph 度會得到一幅 binomial distribution。

而期望值,或者叫平均值,喺呢度講緊嘅係擲中公嘅次數,亦即係 10 * 0.5 = 5 次。
擲幾多次唔撚關事
買六合彩同一個道理 一係中 一係唔中

但係數學計唔到個幣停係中間

個或然撚呢就
你個樣就撚
計 x 次公機率嘅公式係呢條
括號入面嘅 n x 其實係 nCr 嘅另一個寫法,即係 n 個入面抽 x 個有幾多 combinations。
呢如計 P(X = 5) = 10C5 * 0.5^5 * 0.5^5 = 0.2461
上面已經有巴打計到
屌原來我講漏咗
p 係每擲中公嘅機率,q 係每次擲中字嘅機率,因為 p 同 q 係 complementary 所以 q = 1 - p。
計多個例子。
如果要計擲到 2 次或以下公嘅機率 P(X ≤ 2)
= P(X = 0) + P(X = 1) + P(X = 2)
= 10C0 * 0.5^0 * 0.5^10 + 10C1 * 0.5^1 * 0.5^9 + 10C2 * 0.5^2 * 0.5^8
= 0.0547
可能我認真咗
巴打你計錯晒喎
巴打你計錯晒喎
咁應該係點計?




