[學術台] 基礎Finance知識 - Cost of Equity and CAPM

Cost of Equity and CAPM

Imagine you have a friend called Yor.

He is now saving his money in the Bank of China with 1% interest rate per year.
You are running a super risky business which can earn 1% profit for owners or investors per year.

Can you convince Yor to withdraw his money from the bank to invest in your risky business?

No! If your business is much riskier than the bank, he would want to get an average return much higher than 1% for investing in your company.

So the question is:
How much average percentage return should you offer Yor to persuade him to take the risk of investing in your company?

That percentage is called investors’ expected return.
It is also called Cost of Equity.

We can calculate it using CAPM.

CAPM: Capital Asset Pricing Model

Formula:

Explanation for CAPM:
------------------
1. Risk free rate (Rf):
Imagine I offer you a chance to earn money without having risk.
By putting your money into my bank which is protected by the government (the bank won’t collapse!), you can earn 2% return per year.
We call that 2% rate of return -> 2% RISK-FREE RATE

For stocks, the market in U.S. is usually represented as the S&P 500 (Hang Seng Index for Hong Kong market).
------------------
2. Expected Market Return (Rm) in CAPM:
It is just a rate of return you can get by investing in the general stock market

For stocks, the market in U.S. is usually represented as the S&P 500 (Hang Seng Index for Hong Kong market).
------------------
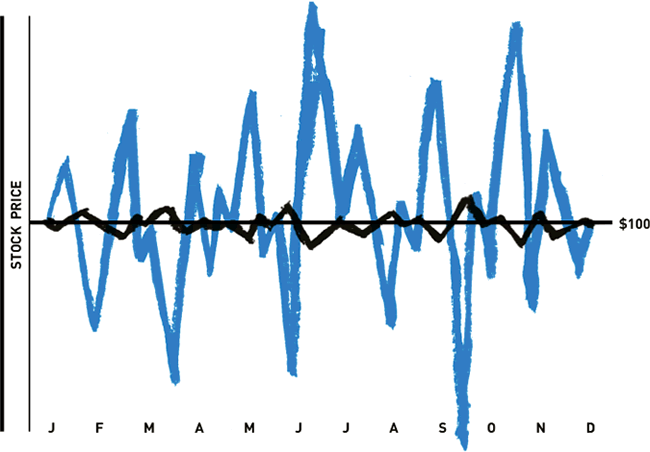
3. Beta, β
β is a way to measure risk using “volatility”(波幅, it is a rate at which the price of a security increases or decreases) compared to a commonly used system, e.g. the general stock market.

High volatility:


Low volatility:


Example: If the beta of Google stock is 1.1,
that means when the general stock market goes up by 20%,
then Google stock will go up by around 22% (1.1 times of the increase), vice versa

Beta = 1.1
=> 10% more volatility (riskier than investing in the general stock market)
When the general stock market goes up/down by 20%,
the stock with beta 1.1 will go up/down by 22% (10% more volatility than the stock market)

If the beta of Google stock is exactly 1.0,
it means when the general stock market goes up by 10%,
the Google stock increases exactly by 10% (same volatility as the general stock market)

In other words, if Beta of a stock is higher,
then its stock price increases more (decreases more) than the general stock market when the general stock market goes up (goes down). So it incurs higher risk!
------------------
4. Market premium (Rm-Rf): the return of the market in excess of the risk-free rate
It is the return in excess of the risk free rate which must be earned by equities to convince investors to take on the risk inherent in them.
------------------

A simple example from Investopedia:

Example of CAPM
Using the CAPM model and the following assumptions, we can compute the expected return for a stock:

The risk-free rate is 2% and the beta (risk measure) of a stock is 2.
The expected market return over the period is 10%, so that means that the market risk premium is 8% (10% - 2%) after subtracting the risk-free rate from the expected market return.
Plugging in the preceding values into the CAPM formula above, we get an expected return of 18% for the stock:
18% = 2% + 2 x (10%-2%)

[學術台] 基礎Finance知識 - WACC:
https://lihkg.com/thread/211478/page/1?post=d262c9192b4aa997c3d71206abf16847ca8b4f88

β is a way to measure risk using “volatility”(波幅, it is a rate at which the price of a security increases or decreases) compared to a commonly used system, e.g. the general stock market.

Not very precise as "volatility" can be the total vol.

beta is the volatility correlated with the market in a security relative to the market volatility

and in CAPM, we measure vol. of returns instead of price.