[數撚圍爐區] 讀萬卷書不如戴口罩

1001 回覆
14 Like 4 Dislike
2020-02-01 16:13:08
2020-02-01 16:17:43
2020-02-01 16:19:38
2020-02-01 16:22:16
2020-02-01 16:24:17
2020-02-01 16:27:11
2020-02-01 16:27:35
2020-02-01 17:16:03
total energy = kinetic energy + potential energy
2020-02-01 18:44:21
我想知佢點derive orbital既形狀出來，不過應該好深
2020-02-01 18:49:56
2020-02-01 18:59:52
2020-02-01 19:01:54
2020-02-01 19:02:49
2020-02-01 19:11:44
2020-02-01 19:55:35
2020-02-01 20:03:02
其實唔難
Schrödinger equation time-independent嗰忽係類似wave equation嘅物體
所以你會得到一啲睇落好似sin, cos咁嘅sinusoidal function
然後你發現你個system (e.g. 你粒atom) 會有啲boundary condition，例如你圍住粒atom轉一個圈，條function唔會變 (i.e. f(0) = f(2π))
於是你就得返一堆discrete嘅solution
而個solution function個frequency越高，energy就越高 (energy = eigenvalue of solution function)
所以高energy嘅solution就會穿過原點好多次
而粒particle嘅probability density係wave function 嘅norm square，所以係個wave function係零嘅地方你就唔會搵到粒particle，我地叫呢啲地方做node
以atom嘅情況嚟計，一個orbital嘅energy就只係depends on佢有幾多個node
記住spherical coordinate (r, θ, φ) 有三樣野，分别係radial, latitudinal 同埋 longitudinal
所以你啲node可以揀擺喺radial, latitudinal或者longitudinal度


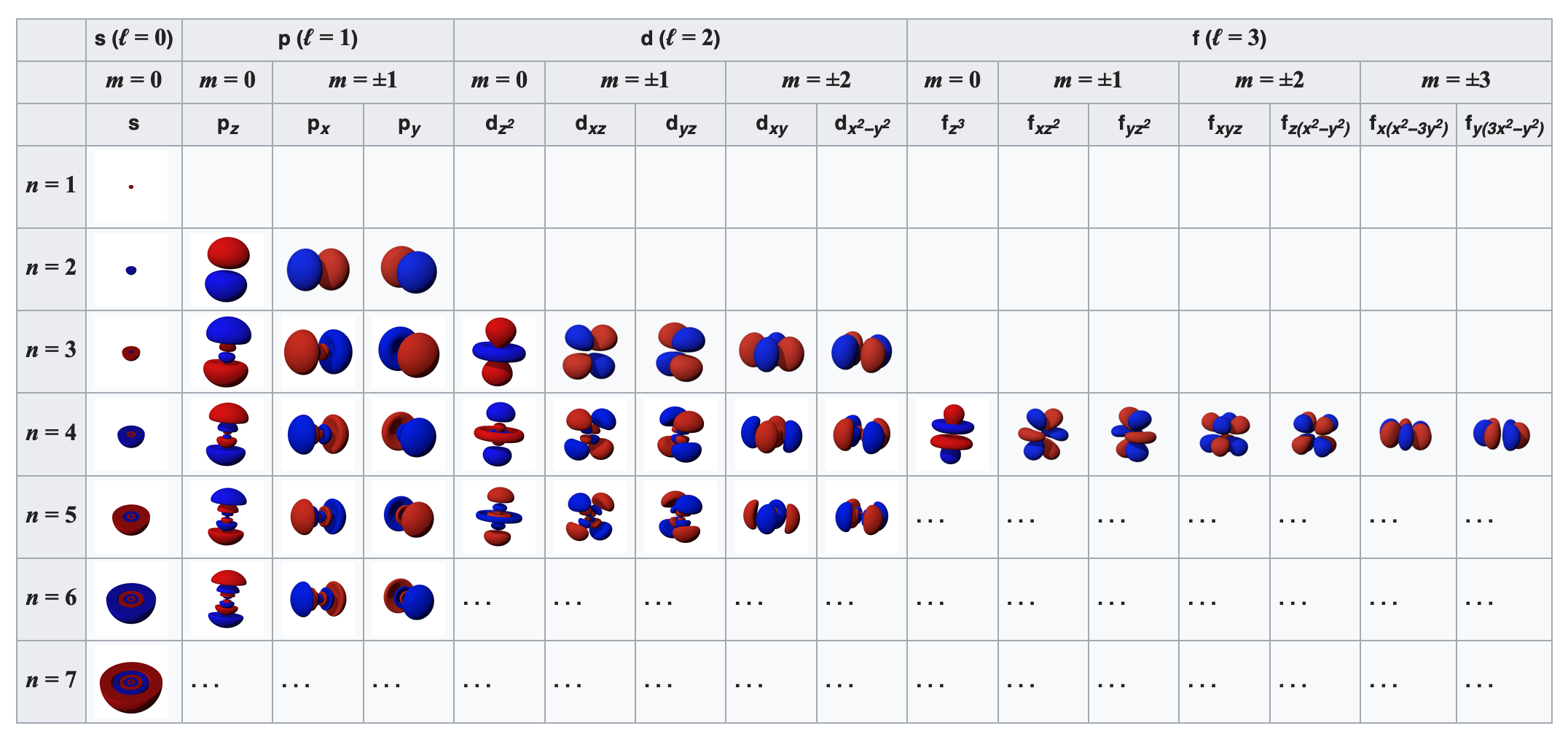
呢度個 n 代表個orbital係第幾低energy
所以最低energy (冇node) 就對應 n=1
而 n=k嘅 orbital就有k-1個node

之後 s,p,d,f 就係數吓有幾多個non-radial node
s代表冇node，p代表一個node，如此類推

而最尾個m就代表個orbital有幾多個longitudinal node
m = 0 就冇node, m = 1, -1就一個node (有longitudinal node嘅時候我地有兩個solution)

咁樣就砌到曬所有你見過嘅atomic orbital
2020-02-01 20:08:22
吹水台自選台熱　門最　新手機台時事台政事台World體育台娛樂台動漫台Apps台遊戲台影視台講故台健康台感情台家庭台潮流台美容台上班台財經台房屋台飲食台旅遊台學術台校園台汽車台音樂台創意台硬件台電器台攝影台玩具台寵物台軟件台活動台電訊台直播台站務台黑　洞